Государственное образовательное учреждение
Среднего профессионального образования
Волгодонский педагогический колледж
Допущена к защите
“____”____________200__г. Защищена с отметкой:______
Зам. директора по управлению Протокол ИГА №__________
образовательным процессом ________________________
________________________
Выпускная квалификационная работа
Тема: «Алгебраические уравнения с одной неизвестной и способы их решения в основной школе»
Специальность: 050201_Математика
Выполнил(а):
студент(ка)
Руководитель:
Волгодонск 2007 г.
СОДЕРЖАНИЕ
Введение……………………………………………………………………......3
ГЛАВА I. Теоретические особенности алгебраических уравнений.
§1. Уравнения с одним неизвестным. Корень уравнения…………...6
§2. Линейные уравнения………………………………………………....10
§3. Квадратные уравнения. Теорема Виета (прямая и обратная)…….......13
§4. Разложение квадратного трехчлена на множители……………….......21
§5. Уравнения, приводимые к линейным и квадратным………………23
§6. Уравнения третей степени…………………………………………...26
§7. Уравнения четвертой степени……………………………………….29
§8. Уравнения, содержащие неизвестное под знаком абсолютной
величины………………………………………………………………32
ГЛАВА II. Использование способов решения алгебраических уравнений на педагогической практике.
§1. Задачи, условия и этапы организации экспериментальной работы по
внедрению алгебраических уравнений на уроках математики в 8 классах…………………………………………………………….34
§2. Эффективность использования разработанной системы………......41
Заключение…………………………………………………………………........43
Список литературы………………………………………………………….......44
Приложения……………………………………………………………………...46
Введение
Велика роль математики в современном мире. Она занимает почетное место в сложном и бурном процессе развития человеческого общества и сама становится производительной силой. Практика наших дней оказывается богатейшим источником новых типов математических задач. Все эти задачи не только выдвинули физические, инженерные и технологические проблемы, но и привели к созданию новых разделов математики, таких как программирование для ЭВМ, ветвящиеся случайные процессы, теория оптимального уравнения и многие другие.
Сегодня понятие «алгебраические уравнения» стало необходимым элементом общей математической культуры. При этом учащиеся должны не только знать основные определения данного материала, но и осознавать необходимость глубокого изучения алгебраических уравнений, их решений. Изучение уравнений способствует расширению кругозора учащихся, улучшению качества их знаний и помогает при поступлении в ВУЗы. Поэтому актуальностью исследования является изучение и решение алгебраических уравнений.
Рассмотрение этого вопроса в научно-методической литературе не решает проблемы по изучению данного материала в школьном курсе математики. Во-первых, не выделяется достаточно времени на более глубокое изучение исследуемых понятий; во-вторых, программой не предусмотрен достаточно подробный разбор уравнений, их решений в основной общеобразовательной школе, которые содействуют развитию математического мышления, формированию научного мировоззрения.
На современном этапе развития общества к математике предъявляются серьезные требования с технологизацией и информатизацией.
Поэтому проблему нашего исследования мы видим в необходимости систематизации и углубления знаний учащихся по данному материалу и отсутствии системности при изучении этого материала в курсе основной школы, что не позволяет сделать процесс обучения оптимальным.
Объект исследования: процесс обучения математики в основной общеобразовательной школе.
Предмет исследования: алгебраические уравнения и способы их решения как составляющая курса обучения математики.
Цель исследования: изучить в теории и практике способы решения алгебраических уравнений с одним неизвестным, выявить методические условия, способствующие повышению знаний, умений и навыков учащихся по решению различных видов алгебраических уравнений и апробировать их на практике.
Исходя из поставленных целей исследования, вытекают следующие задачи:
1. Выявить различные виды и способы решения алгебраических уравнений с одним неизвестным.
2. Определить методологические условия, способствующие качественному формированию знаний, умений и навыков в решении алгебраических уравнений.
3. Апробировать на практике в основной школе различные способы решения алгебраических уравнений.
Гипотеза: системное изложение учебного материала по алгебраическим уравнениям в курсе основной общеобразовательной школы будет способствовать углублению и оптимизации знаний по математике и созданию прочной базы для усвоения курса высшей математики.
Методологической основой нашего исследования явилась гуманистическая личностно-ориентированная концепция обучения, которая позволяет поставить потребности учащихся в центре всей педагогической системы.
Теоретическая значимость: на основе теоретического обобщения научно-методических источников выявлен наиболее оптимальный способ решения алгебраических уравнений с одним неизвестным.
Методы исследования: анализ научно-методической литературы по проблеме исследования, методы эмпирического исследования: наблюдение, анкетирование, контрольные задания, экспериментальные методы статистической обработки результатов.
База исследования: теоретические разработки исследования апробировались в 8 классе средней общеобразовательной школы №4 Мартыновского района, хутора Малоорловский.
ГЛАВА I. Теоретические особенности алгебраических уравнений.
Уравнения с одним неизвестным. Корень уравнения.
Буквенные величины, входящие в равенство двух выражений 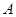 и
и 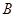 :
: 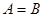 , по условию задачи могут быть неравноправными. Одни из них считаются известными, или параметрами. Они могут принимать все свои допустимые значения. Другие буквенные величины являются неизвестными.
, по условию задачи могут быть неравноправными. Одни из них считаются известными, или параметрами. Они могут принимать все свои допустимые значения. Другие буквенные величины являются неизвестными.
Равенство, содержащее неизвестные числа, обозначенные буквами, называется уравнением.
В зависимости от числа неизвестных, входящих в уравнение, рассматривают уравнения с одним, с двумя и т.д. неизвестными.
Неизвестные величины в уравнениях обычно обозначают буквами 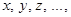 а известные (или параметры) – буквами
а известные (или параметры) – буквами 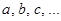
Будем сначала рассматривать уравнение с одним неизвестным 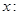
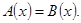
Выражения, стоящие слева и справа от знака равенства, называются левой и правой частями уравнения. Каждое слагаемое части уравнения называется членом уравнения.
Областью допустимых значений (сокращенно ОДЗ) или областью определения уравнения 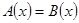 называется множество всех числовых значений неизвестного
называется множество всех числовых значений неизвестного 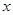 , при каждом из которых имеют смысл выражения
, при каждом из которых имеют смысл выражения 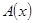 и
и 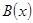 одновременно.
одновременно.
Определение. Корнем (или решением) уравнения называется то значение неизвестного, при котором это уравнение обращается в верное равенство. [20, c.34]
Очевидно, что корень уравнения принадлежит ОДЗ этого уравнения.
Решить уравнение - это значит найти все его корни или установить, что их нет.
Например, уравнение 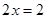 имеет единственный корень
имеет единственный корень 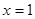 ; уравнение
; уравнение 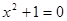 не имеет корней во множестве R: для любого действительного числа
не имеет корней во множестве R: для любого действительного числа 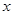 всегда
всегда 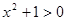 .
.
Определение. Два уравнения называются равносильными (эквивалентными), если всякий корень одного уравнения является корнем другого, и наоборот. Если оба уравнения не имеют корней (решений), то они также считаются равносильными. [20, c.34]
Иначе говоря, равносильными называются уравнения, множества корней которых совпадают.
Если уравнения 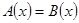 и
и 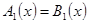 равносильны, то пишут
равносильны, то пишут 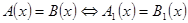 .
.
Например, 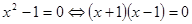 ;
; 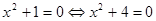 , так как эти уравнения не имеют действительных корней. Ясно, что уравнения
, так как эти уравнения не имеют действительных корней. Ясно, что уравнения 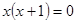 и
и 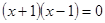 неравносильны.
неравносильны.
При решении уравнения путем различных преобразований стараются заменить его более простым, равносильным ему уравнением. Однако такая замена не всегда удается. Тогда возможны следующие два случая:
1. При переходе к новому уравнению может произойти потеря корней. Например, при переходе от уравнения 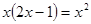 к уравнению
к уравнению 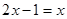 сокращением на неизвестное
сокращением на неизвестное 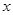 происходит потеря корня
происходит потеря корня 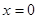 . Поэтому при переходе к новому уравнению надо учитывать возможность потери корня данного уравнения.
. Поэтому при переходе к новому уравнению надо учитывать возможность потери корня данного уравнения.
2. Новое уравнение может содержать корни, не являющиеся корнями
данного уравнения (так называемые посторонние корни). Например, при переходе от уравнения 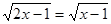 к уравнению
к уравнению 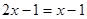 возведением в квадрат обеих частей исходного уравнения получим
возведением в квадрат обеих частей исходного уравнения получим 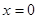 - посторонний корень этого уравнения. Поэтому часто делают проверку корней, подставив их в данное уравнение.
- посторонний корень этого уравнения. Поэтому часто делают проверку корней, подставив их в данное уравнение.
Напомним, что числовые равенства обладают следующими свойствами:
1) числовое равенство не нарушится, если к обеим его частям прибавить
одно и то же число;
2) числовое равенство не нарушится, если обе его части умножить или
разделить на одно и то же число, отличное от нуля.
Из свойств числовых равенств и понятия равносильных уравнений вытекают следующие основные свойства уравнений:
1) Уравнение 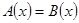 , (1) равносильно уравнению
, (1) равносильно уравнению 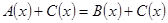 , (2) где
, (2) где 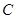 - число или некоторое выражение, имеющее смысл на множестве допустимых значений (т.е. на ОДЗ) уравнения
- число или некоторое выражение, имеющее смысл на множестве допустимых значений (т.е. на ОДЗ) уравнения 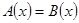 .
.
Доказательство:
Обозначим через 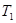 множество решений уравнения (1), а через
множество решений уравнения (1), а через 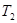 множество решений уравнения (2). Тогда уравнения (1) и (2) будут равносильны, если
множество решений уравнения (2). Тогда уравнения (1) и (2) будут равносильны, если 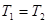 . Но чтобы убедиться в этом, необходимо показать, что любой корень из
. Но чтобы убедиться в этом, необходимо показать, что любой корень из 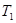 является корнем уравнения (2) и, наоборот, любой корень из
является корнем уравнения (2) и, наоборот, любой корень из 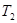 является корнем уравнения (1).
является корнем уравнения (1).
Пусть число 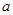 -корень уравнения (1). Тогда
-корень уравнения (1). Тогда 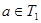 и при подстановке в уравнение (1) обращает его в истинное числовое равенство
и при подстановке в уравнение (1) обращает его в истинное числовое равенство 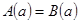 ,а выражение
,а выражение 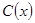 обращает в числовое выражение
обращает в числовое выражение 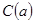 . Прибавим к обеим частям истинного равенства
. Прибавим к обеим частям истинного равенства 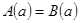 числовое выражение
числовое выражение 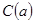 . Получим согласно свойствам истинных числовых равенств истинное числовое равенство
. Получим согласно свойствам истинных числовых равенств истинное числовое равенство 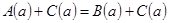 .
.
Но это равенство говорит о том, что число 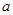 является также и корнем уравнения (2).
является также и корнем уравнения (2).
Итак, доказано, что каждый корень уравнения (1) является корнем и уравнения (2), т.е. 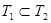 .
.
Пусть теперь 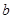 - корень уравнения (2). Тогда
- корень уравнения (2). Тогда 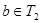 и при подстановке в уравнение обращает его в истинное числовое равенство
и при подстановке в уравнение обращает его в истинное числовое равенство 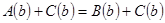 .
.
Прибавим к обеим частям этого равенства числовое выражение 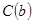 . Получим истинное числовое равенство
. Получим истинное числовое равенство 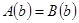 , которое говорит о том, что число
, которое говорит о том, что число 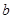 - корень уравнения (1).
- корень уравнения (1).
Итак, доказано, что каждый корень уравнения (2) является и корнем уравнения (1), т.е. 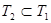 .
.
Так как 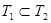 и
и 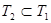 , то по определению равных множеств
, то по определению равных множеств 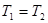 , а значит, уравнения (1) и (2) равносильны, ч.т.д.
, а значит, уравнения (1) и (2) равносильны, ч.т.д.
Следствие. Любое слагаемое можно перенести из одной части уравнения в другую с противоположным знаком.
Например, 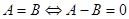 .
.
2) Уравнение 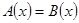 равносильно уравнению
равносильно уравнению 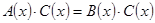 , где
, где 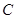 - число или некоторое выражение, имеющее смысл на множестве допустимых значений уравнения
- число или некоторое выражение, имеющее смысл на множестве допустимых значений уравнения 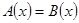 и не обращающееся на нем в нуль.
и не обращающееся на нем в нуль.
Доказательство этого свойства аналогично доказательству свойства 1.
Следствие. Обе части уравнения можно сокращать на общий множитель, не обращающийся в нуль на множестве допустимых значений
данного уравнения.
Действительно, уравнение 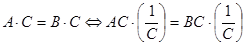 , т.е.
, т.е.
равносильно уравнению 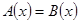 .
.
3) Уравнение 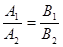 равносильно уравнению
равносильно уравнению 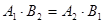 , рассматриваемому на множестве допустимых значений исходного уравнения
, рассматриваемому на множестве допустимых значений исходного уравнения 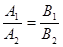 или на своем множестве при дополнительном условии
или на своем множестве при дополнительном условии 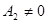 ,
, 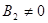 .
.
Эти свойства используются при решении уравнений. [5, c.116]
Линейные уравнения.
Определение. Уравнением первой степени с одним неизвестным называется уравнение вида 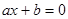 , где
, где 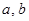 - заданные числа, причем
- заданные числа, причем 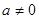 , а
, а 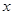 - неизвестное.
- неизвестное.
При этом число 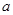 называется коэффициентом при неизвестном
называется коэффициентом при неизвестном 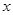 ,
,
число 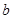 - свободным членом уравнения.
- свободным членом уравнения.
Это уравнение равносильно уравнению 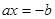 , из которого получаем, что
, из которого получаем, что 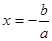 . Таким образом, уравнение первой степени всегда имеет единственный корень
. Таким образом, уравнение первой степени всегда имеет единственный корень 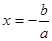 .
.
Уравнение первой степени является частным случаем линейного уравнения 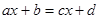 , где
, где 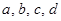 - заданные числа, а
- заданные числа, а 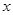 - неизвестное.
- неизвестное.
Линейное уравнение сводится к равносильному ему уравнению вида 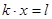 , где
, где 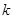 и
и 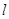 - известные числа. При этом число
- известные числа. При этом число 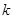 - коэффициент при неизвестном
- коэффициент при неизвестном 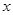 , может оказаться равным нулю, в отличие от коэффициента при неизвестном в уравнении первой степени.
, может оказаться равным нулю, в отличие от коэффициента при неизвестном в уравнении первой степени.
Может оказаться, что линейное уравнение не имеет корней или имеет бесконечное множество корней. [5, с.118]
Пример 1. Показать, что уравнение 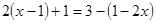 не имеет корней.
не имеет корней.
Решение. Данное уравнение равносильно уравнению
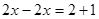 или
или 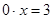 .
.
Это уравнение не имеет корней, так как левая часть 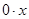 равна нулю при любом
равна нулю при любом 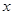 , а значит, не равна 3. [1, c.34]
, а значит, не равна 3. [1, c.34]
Пример 2. Решить уравнение 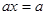 .
.
Решение. Это уравнение содержит параметр 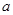 (переменную, которая в условии данной задачи сохраняет одно и то же значение).
(переменную, которая в условии данной задачи сохраняет одно и то же значение).
Если 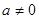 , то
, то 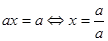 , т.е.
, т.е. 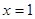 - единственный корень уравнения. Если
- единственный корень уравнения. Если 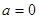 , то уравнение принимает вид
, то уравнение принимает вид 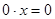 и его корнем является любое действительное число
и его корнем является любое действительное число 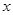 . [1, c.35]
. [1, c.35]
Пример 3. Решить уравнение
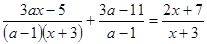 .
.
Решение.
1) После приведения дробей к общему знаменателю 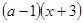 получим линейное уравнение
получим линейное уравнение 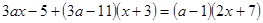 , равносильное исходному, при условии, что
, равносильное исходному, при условии, что 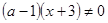 , т.е.
, т.е. 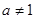 ,
, 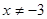 .
.
2) После приведения подобных членов и сведения полученного уравнения к стандартному для линейного уравнения виду 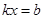 имеем
имеем 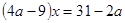 , (*)
, (*)
3) а) Если 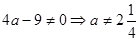 , то
, то 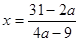 . Теперь необходимо исключить те значения параметра
. Теперь необходимо исключить те значения параметра 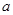 , при которых найденное значение
, при которых найденное значение 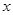 равно
равно 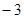 , чего не может быть по области определения (ОДЗ) исходного уравнения. Приравняем дробь
, чего не может быть по области определения (ОДЗ) исходного уравнения. Приравняем дробь 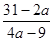 к
к 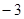 :
:
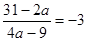 ,
, 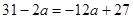 ,
, 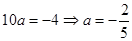 .
.
Таким образом, при 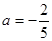 полученное в результате преобразования линейное уравнение имеет корень
полученное в результате преобразования линейное уравнение имеет корень 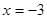 , посторонний для исходного уравнения.
, посторонний для исходного уравнения.
б) Если 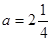 , то уравнение (*) примет вид
, то уравнение (*) примет вид 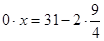 или
или 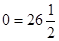 - неверное равенство, т.е. уравнение (*) не имеет корней.
- неверное равенство, т.е. уравнение (*) не имеет корней.
Вообще, если уравнение не имеет корней, то говорят также, что множество корней уравнения пустое, и обозначают Ø.
Ответ. 1) При 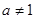 ,
, 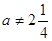 и
и 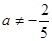 уравнение имеет единственное решение
уравнение имеет единственное решение 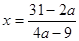 ;
;
2) при 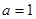 данное уравнение не имеет смысла;
данное уравнение не имеет смысла;
3) при 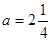 и
и 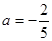 нет решений.
нет решений.
Ответ можно записать короче:
1) если 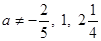 , то
, то 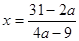 ; 2) если
; 2) если 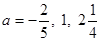 , то Ø. [14, c.42]
, то Ø. [14, c.42]
 2020-01-14
2020-01-14 551
551







