2020-01-14
147
Перейдем к исследованию уравнения
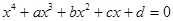, (1)
четвертой степени. Рассмотрим его способ.
Перенесем три последних члена уравнения (1) в правую часть и прибавим к обеим частям 
Тогда получится:
Затем прибавляем к обеим частям последнего уравнения сумму
Уравнение примет вид:
, (2)
Подберем вспомогательное неизвестное 
так, чтобы правая часть последнего уравнения превратилась в полный квадрат. Это будет очевидно, в том случае, когда
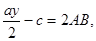
Но 
Поэтому должно быть:
Если раскрыть скобки, то после некоторых преобразований получится также уравнение третьей степени относительно y:
Пусть 
какой-нибудь корень этого уравнения. Подставляя его в уравнение (2), превратим его правую часть в полный квадрат 
Отсюда
или
Эти два квадратных уравнения и дадут нам все четыре корня уравнения четвертой степени. [24, c.112]
Итак, решение уравнения четвертой степени сводится к решению одного уравнения третьей степени и двух уравнений второй степени.
Пример. Найдем корни уравнения
Здесь 
, 
, 
, 
. Следовательно, y должно удовлетворять уравнению
Приводим последнее уравнение к трехчленному виду, полагая в нем
Получаем 
откуда 
а потому 
Затем находим 
и 
.
Мы видим, что и имеют положительные знаки, так как произведение 
отрицательно. Поэтому полагаем 
, 
(с таким же успехом можно было взять 
, 
). Отсюда получаются такие квадратные уравнения:
или
Решая первое уравнение, получаем 
Решая второе уравнение, получаем 
Уравнения, содержащие неизвестное под знаком
Абсолютной величины.
Эти уравнения можно свести к уравнениям, не содержащим знака абсолютной величины, используя ее определение. Так, решение уравнения
, (1)
сводится к решению двух уравнений с дополнительными условиями.
1. Если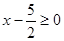 
, то уравнение (1) приводится к виду
, (2)
Решения этого уравнения: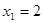 
, 
. Условию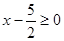
удовлетворяет лишь второй корень квадратного уравнения (2), и, следовательно, число 3 является корнем исходного уравнения (1).
2. Если 
, то уравнение (1) приводится к виду
.
Корнями этого уравнения будут числа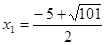 
и 
. Первый корень 
не удовлетворяет условию 
и поэтому не является решением уравнения (1).
Таким образом, решениями уравнения (1) будут числа 3 и 
.
Заметим, что коэффициенты уравнения, содержащего неизвестное под знаком абсолютной величины, можно подобрать так, что решениями будут все, значения неизвестного, принадлежащие некоторому промежутку числовой оси. Например, решим уравнение
, (3)
Отметим на числовой оси точки 0 и 3 (нули функций, стоящих под знаком абсолютной величины). Эти точки разобьют числовую
ось на три промежутка (рис. 1):
; 
; 
На этих промежутках:
1) при 
уравнение (3) приводится к виду 
и в промежутке 
решений не имеет.
0 3 х
Рис. 1
Аналогично при 
уравнение (3) приводится к виду 
и в промежутке 
решений не имеет;
2) при 
уравнение (3) приводится к виду 
, т.е. обращается в тождество. Следовательно, любое значение 
является решением уравнения (3). [23, 110]
