2020-01-14
129
Будем рассматривать уравнение третей степени вида 
, где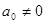 
, 
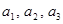- любые коэффициенты. Левая часть – это многочлен третей степени, поэтому уравнение имеет три корня (возможно комплексные и совпадающие). Разделим данное уравнение на 
, тогда получим:
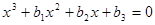, (1)
Преобразуем это уравнение так, чтобы исчез член с квадратом неизвестного. Если положить
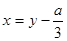
и подставить это выражение в наше уравнение, то после несложных выкладок получится более простое уравнение
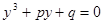, (2)
которое называется приведенным уравнением третей степени.
Таким образом, остается решить уравнение (2). Полагаем 
, где 
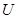и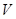 
– два новых вспомогательных неизвестных, и, подставляя это выражение 
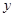в уравнение (2), мы получим:
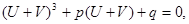
или, раскрыв скобки и перегруппировав члены:
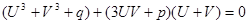, (3)
Так как вместо одного неизвестного ввели две неизвестные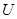 
и 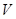, то одно может быть выбрано произвольно, т.е. между 
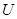и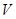 
можем установить еще одну произвольную зависимость. Потребуем, чтобы 
.
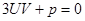Значит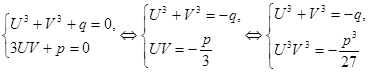 
Мы видим, что 
и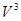 
являются корнями приведенного квадратного уравнения
Решая это уравнение, находим:
откуда
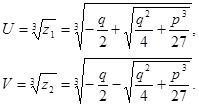
Итак, неполное уравнение (2) нам удалось решить алгебраически:
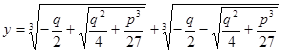, (4)
Формула (4) называется формулой Кардана.
По этой формуле получается девять значений, а нас интересует только три значения. Нужные три значения найдем из условия
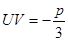, (5)
Чтобы упростить систему поисков, поступим следующим образом: обозначим через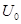 
одно из значений 
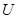(любое), а через 
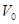такое значение 
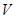, чтобы 
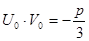или 
. Тогда остальные значения находятся по формулам:
, 
,
, 
.
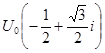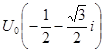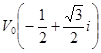Таким образом, получаем все три корня уравнения (2):
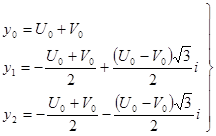(6)
Пример. Определить по формуле Кардана корни уравнения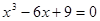 
.
Здесь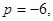 
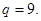Следовательно,
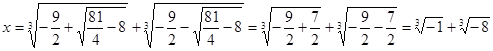
Отсюда по формулам (6) получаем три корня уравнения:
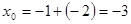
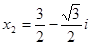[23, c.99].
