Вычисление площади многоугольника по координатам его вершин

Метод координат, предложенный в XVII веке французскими математиками Р. Декартом (1596-1650) и П. Ферма (1601-1665), является мощным аппаратом, позволяющем переводить геометрические понятия на алгебраический язык. В основе этого метода лежит понятие – система координат. Мы будем рассматривать вычисление площади многоугольника по координатам его вершин в прямоугольной системе координат.

Площадь треугольника

Теорема 1. Если 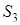 - площадь треугольника

 

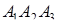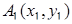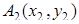, где ,  и ,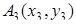

 

то справедливо равенство

 

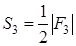,                                    (1.8)

 

где .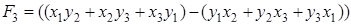

 

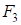 будем называть определителем площади треугольника.

Доказательство. Пусть вершины 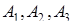 треугольника расположены в первой координатной четверти. Возможны два случая.

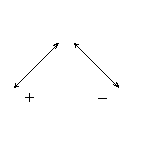
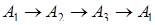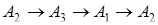Случай 1. Направление  (или , или 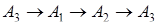) расположения вершин треугольника совпадает с направлением движения конца часовой стрелки (рис. 1.30).

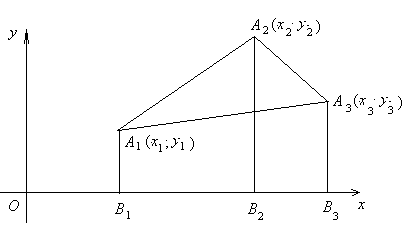
Рис. 1.30

 

Имеем:

 

.

 

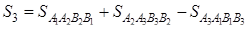Но

 

,

 

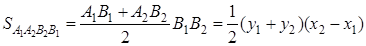Так как фигура 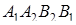 - трапеция.

Аналогично находим, что

 

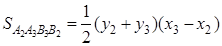 и .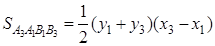

 

Выполнив алгебраические преобразования

,

 

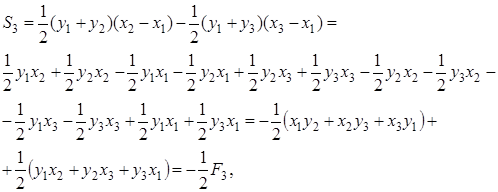 получим, что:

 

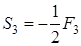.                                            (1.9)

 

В равенстве (1.9) определитель площади 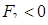, о поэтому перед выражением стоит знак «минус», так как .

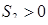Покажем, что 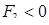. Действительно, здесь

 

 

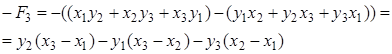
так как

 

 

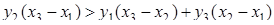
(площадь прямоугольника с основанием 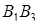 и высотой  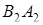больше суммы площадей прямоугольников с основаниями 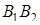,  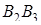и высотами 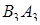, 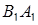; (рис. 1.30), откуда

 

.

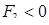Случай 2. Указанные направления в случае 1 противоположны направлению движения конца часовой стрелки (рис. 1.31)

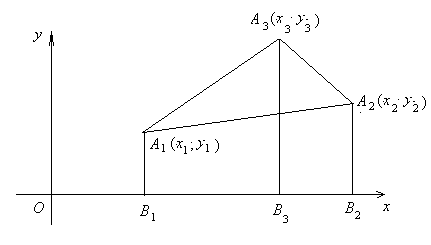
Рис. 1.31

 

Здесь

 

.

 

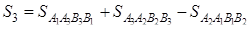Но

,

 

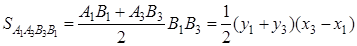так как фигура 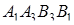 - трапеция, а

 

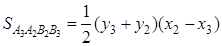 и .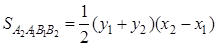

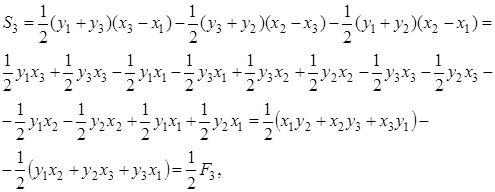
получим:

 

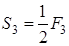,                                       (1.10)

 

где 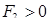. Действительно, здесь

 

 

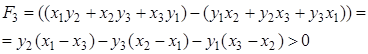
Теорема доказана, когда вершины треугольника расположены в первой координатной четверти.

Воспользовавшись понятием модуля, равенства (1.9) и (1.10) можно записать так:

 

,

 

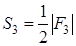так как

 

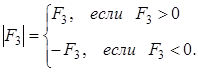
Замечание 1. Мы вывели формулу (1.8), рассматривая простейшее расположение вершин , изображённое на рисунках 1.30 и 1.31; однако формула (1.8) верна при любом расположении вершин .

Рассмотрим случай, изображённый на рисунке 1.32.

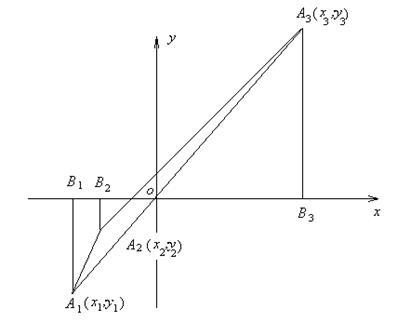
Рис. 1.32

 

Здесь

 

.

 

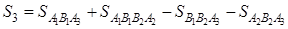Но

 

,

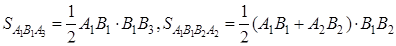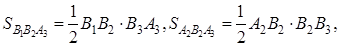
где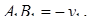  

 

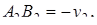
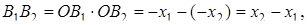
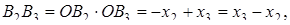
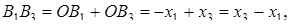
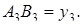
Поэтому, выполнив несложные геометрические преобразования:

 

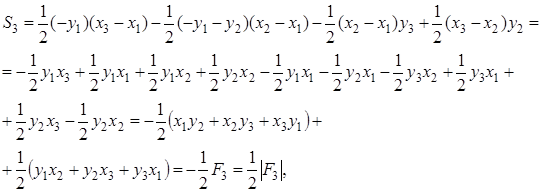
получим снова, что 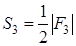, где

 

.

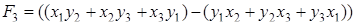Площадь n -угольника

Многоугольник может быть выпуклым или невыпуклым, порядок нумерации вершин считается отрицательным, если вершины нумеруются по направлению движения конца часовой стрелки. Многоугольник, не имеющий самопересечения сторон, будем называть простым. Для простого именно n -угольника справедлива следующая

Теорема 2. Если 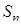 - площадь простого n -угольника 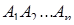, где 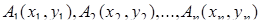, то справедливо равенство

 

,

 

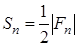где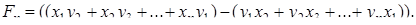

 

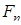 будем называть определителем площади простого n -угольника.

Доказательство. Возможны два случая.

Случай 1. n -угольник – выпуклый. Докажем формулу (1.11) методом математической индукции.

Для 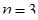 она уже доказана (теорема 1). Предположим, что она справедлива для n -угольника; докажем, что она остаётся справедливой и для выпуклого (n +1)-угольника.

Добавим к многоугольнику 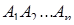 ещё одну вершину  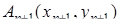(рис. 1.33).

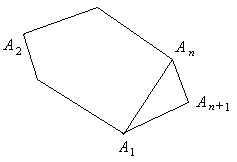
Рис. 1.33

 

Имеем:

 

 

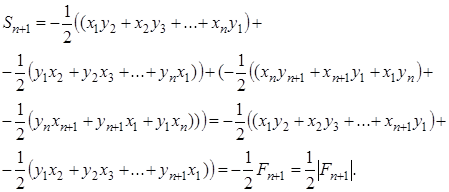
Таким образом, формула справедлива для (n +1)-угольника, и, значит, условия математической индукции выполнены, т. е. формула (1.11) для случая выпуклого n -угольника доказана.

Случай 2. n -угольник – невыпуклый.

В любом невыпуклом n -угольнике можно провести диагональ, лежащую внутри него, и поэтому доказательство случая 2 для невыпуклого n -угольника аналогична доказательству для выпуклого n -угольника.

Замечание 2. Выражения для 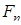 запоминаются нелегко. Поэтому, для вычисления его значений удобно выписать в столбец координаты первой, второй, третьей, …, n -й и снова первой вершин n -угольника и провести умножение по схеме:

 

                      

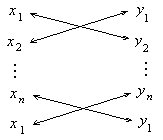
 (1.12)                                   (1.13)

 

Знаки в столбце (1.12) надо расставить так, как указано в схеме (1.13).

Замечание 3. При составлении столбца (1.12) для треугольника можно начать с любой вершины.

Замечание 4. При составлении столбца (1.12) для n -угольника (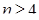) необходимо соблюдать последовательность выписывания координат вершин n -угольника (с какой вершины начинать обход безразлично). Поэтому вычисление площади n -угольника следует начинать с построения «грубого» чертежа.

 

Формула Пика

Чтобы оценить площадь многоугольника на клетчатой бумаге, достаточно подсчитать, сколько клеток покрывает этот многоугольник (площадь клетки мы принимаем за единицу). Точнее, если S – площадь многоугольника, 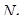 - число клеток, которые целиком лежат внутри многоугольника, и  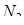- число клеток, которые имеют с внутренностью многоугольника хоть одну общую точку .

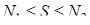Будем рассматривать ниже только такие многоугольники, все вершины которых лежат в узлах клетчатой бумаги – в таких, где пересекаются линии сетки. Оказывается, что для таких многоугольников можно указать такую формулу:

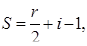
где  - площадь, r – число узлов, которые лежат строго внутри многоугольника.

Эту формулу называют «формула Пика» - по имени математика, открывшего её в 1899 году.

Простые треугольники

Площадь любого треугольника, нарисованного на клетчатой бумаге, легко посчитать, представив её как сумму или разность площадей прямоугольных треугольников и прямоугольников, стороны которых идут по линиям сетки, проходящим через вершины нарисованного треугольника. Проделав это, например, для треугольников, изображённых на рисунке 1.34, можно убедиться, что площадь получается всегда равной «полученному» числу – числу вида 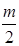, где 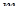 - целое.

 

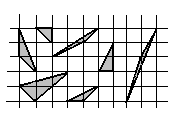
Рис. 1.34

 

Назовём треугольник простым, если ни внутри него, ни на его сторонах нет узлов сетки, за исключением вершин. Все простые треугольники на рис. 1.34 имеют площадь 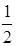. Мы увидим, что это не случайно.

Задача. Три кузнечика (три точки) в начальный момент времени сидят в трёх вершинах одной клетки, а затем начинают «играть в чехарду»: каждый может прыгнуть через одного из двух других, после чего оказывается в симметричной относительно его точке (рис. 1.35, ясно, что после любого числа таких прыжков кузнечики будут попадать в узлы клетчатой бумаги). В каких тройках точек могут через несколько прыжков оказаться кузнечики?

 

                                  

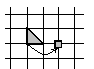
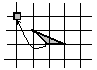
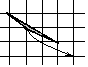
Рис. 1.35

 

Назовём треугольник достижимым, если в его вершинах могут одновременно оказаться три кузнечика, которые вначале были в трёх вершинах одной клетки; прыжком будем называть преобразование треугольника, заключающееся в том, что одна из вершин переходит в точку, симметричную относительно любой из двух других вершин (эти две вершины остаются на месте).

Теорема 1. Следующие три свойства треугольников с вершинами в узлах клетчатой бумаги эквивалентны друг другу:

1) треугольник имеет площадь ,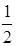

2) треугольник прост,

3) треугольник достижим.

Познакомимся со следующими свойствами простого треугольника, которые и приводят к справедливости данной теоремы.

1. Площадь треугольника при прыжке не меняется.

2. Любой достижимый треугольник имеет площадь .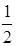

3. Если достроить простой треугольник АВС до параллелограмма ABCD, то ни внутри, ни на сторонах этого параллелограмма не будет узлов (не считая вершин).

4. Из простого треугольника при прыжке получается простой.

5. Из простого треугольника один из углов – тупой или прямой (причём последний случай возможен только для треугольника, у которого три вершины принадлежат одной клетке, такой простой треугольник – со сторонами 1, 1, 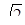 будем называть минимальным.)

6. Из любого простого не минимального треугольника можно одним прыжком получить треугольник, у которого наибольшая сторона меньше, чем наибольшая сторона исходного.

7. Любой простой треугольник можно конечным числом прыжков перевести в минимальный.

8. Любой простой треугольник достижим.

9. Любой простой треугольник имеет площадь .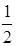

10. Любой треугольник можно разрезать на простые.

11. Площадь любого треугольника равна 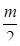, причём при любом разрезании его на простые их количество равно m.

12. Любой треугольник площади 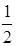 - простой.

13. Для любых двух узлов А и В решётки, на отрезке между которыми нет других узлов, найдётся узел С такой, что треугольник АВС – простой.

14. Узел С в предыдущем свойстве можно всегда выбрать так, что угол АСВ будет тупым или прямым.

15. Пусть клетчатая плоскость разрезана на равные параллелограммы так, что все узлы являются вершинами параллелограммов. Тогда каждый из треугольников, на которые один из этих параллелограммов разрезается своей диагональю – простой.

16. (Обратное 15). Треугольник АВС – простой тогда и только тогда, когда всевозможные треугольники, полученные из АВС параллельными переносами, переводящими узел А в различные узлы решётки, не накладываются друг на друга.

17. Если решётку – узлы клетчатой бумаги – разбить на четыре подрешётки с клетками 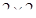 (рис. 1.36), то вершины простого треугольника обязательно попадут в три разные подрешётки (все три имеют разные обозначения).

 

Рис. 1.36

 

Следующие два свойства дают ответ к задаче о трёх кузнечиках.

18. Три кузнечика могут одновременно попасть в те и только те тройки точек, которые служат вершинами простого треугольника и имеют тот же знак, что и соответствующие вершины начального треугольника.

19. Два кузнечика могут одновременно попасть в те и только те пары узлов соответствующих знаков, на отрезке между которыми нет других узлов.