Рассмотрим наполнение бака от 0 до номинального значения расхода с учетом прироста, приданного в линеаризованной модели. Таким образом, рассмотрим скачок u1=0,03; u2=0.
Обозначим 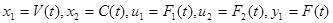 , уравнение бака запишем в виде системы:
, уравнение бака запишем в виде системы:
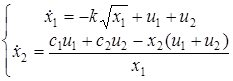
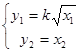
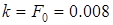
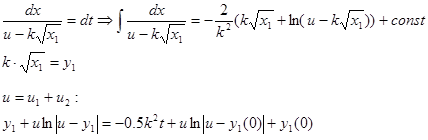
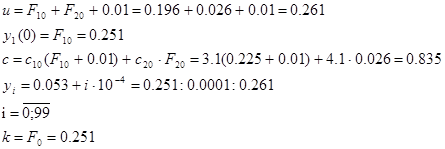
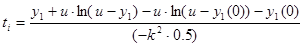
Подставляя 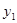 и u=0.063, найдем время, которое соответствует указанным значениям. Сведем результаты в таблицу.
и u=0.063, найдем время, которое соответствует указанным значениям. Сведем результаты в таблицу.
Таблица 1. Линеаризация системы по первому выходу
|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| y1 | 0.251 | 0.252 | 0.253 | 0.254 | 0.255 | 0.256 | 0.257 | 0.258 | 0.259 | 0.26 |
| t | 0 | 0.841 | 1.785 | 2.86 | 4.106 | 5.584 | 7.402 | 9.753 | 13.081 | 18.793 |
Т.к. нет аналитической зависимости 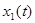 , используем ее кусочно-линейную аппроксимацию, представляя на промежутке от
, используем ее кусочно-линейную аппроксимацию, представляя на промежутке от 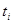 до
до 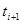 функцию
функцию 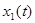 как
как 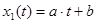 . Тогда,
. Тогда,
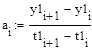
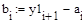
Занесем полученные значения в таблицу:
Таблица 2 Результаты промежуточного расчета
| a | 0.00119 | 0.00106 | 0.00093 | 0.0008 | 0.00068 | 0.00055 | 0.00043 | 0.0003 | 0.00018 |
| b | 0.251 | 0.252 | 0.253 | 0.254 | 0.255 | 0.256 | 0.257 | 0.258 | 0.259 |
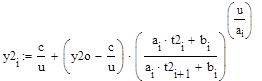
Полученные значения занесем в таблицу:
Таблица 3. Линеаризация системы по второму выходу
| y2 | 3.2012735 | 3.2011172 | 3.2009393 | 3.2007371 | 3.2005089 | 3.2002573 | 3.1999954 | 3.1997612 | 3.1996304 |
| t | 0 | 0.841 | 1.785 | 2.86 | 4.106 | 5.584 | 7.402 | 9.753 | 13.081 |
Получение квадратичной модели
Уравнение квадратичной системы имеет вид:
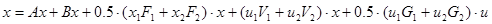
Матрицы с подстановкой номинального режима:
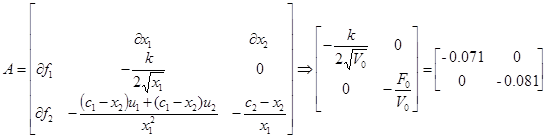
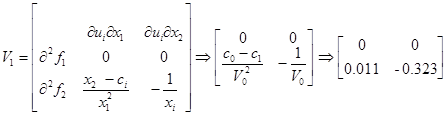
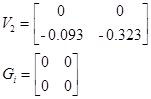
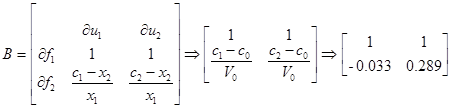
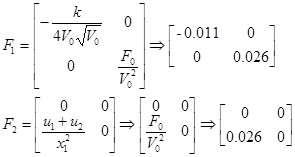
Запись билинейной модели
Уравнение билинейной системы записывается в виде
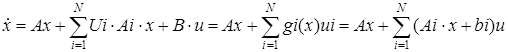
Приняв допущение, что критерий оптимальности в форме О.А. Красовского
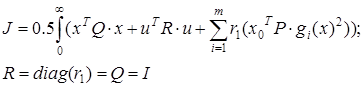
регулятор определяется по зависимости 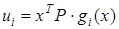
Где матрица определена как 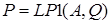
Линеаризованная модель
Линеаризуем зависимость 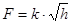 , разложив ее на ряд Тейлора.
, разложив ее на ряд Тейлора.
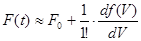

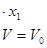
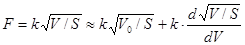
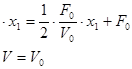
С учетом ранее изложенного запишем:
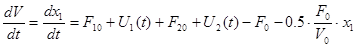
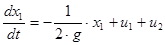 ; (т.к.
; (т.к. 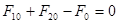 ), где
), где 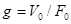 ;
;
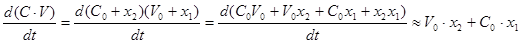
Припустив в случае остатка 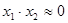 . Тогда, подставив производную
. Тогда, подставив производную 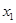 , получим
, получим
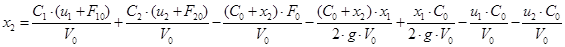
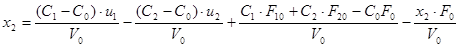
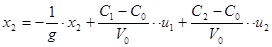
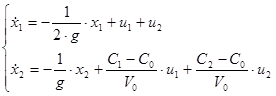
Представим систему в матричной форме:
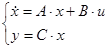
Тогда матрицы А и В запишутся в виде
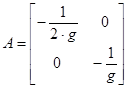 ,
, 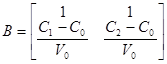
Для определения матрицы С необходимо установить связь между векторами x и y. Т.к. 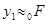 ,
, 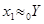 , то
, то
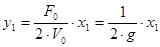 ;
; 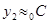
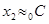 , то
, то 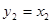
Тогда
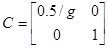
Система будет иметь вид
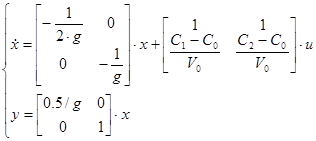
Коэффициенты модели системы:
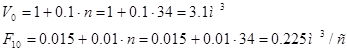

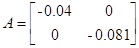
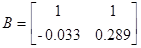
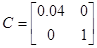
Модель в дискретном времени
Система в дискретном времени имеет вид:
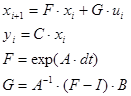
dt= 24 c.
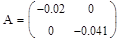
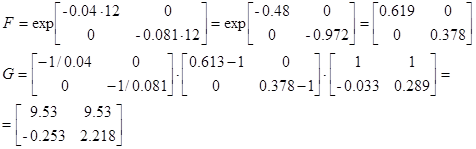
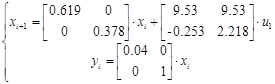
Зададим 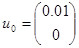 ,
, 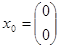 , получим значения на выходах дискретной системы.
, получим значения на выходах дискретной системы.
Таблица 4 Значение выходов дискретной системы
| Возмущение | Реакция выхода системы y(t) | |||||||
| u1=0.01 u2=0 | y1 y2 | 0 0 | 0.00384 -0.00254 | 0.00624 -0.00352 | 0.0077 -0.03896 | 0.00859 -0.004038 | 0.00913 -0.00409 | 0.00947 -0.00411 |
| время t, с | 0 | 12 | 24 | 37 | 49 | 61 | 74 | |
Преобразование модели в форме Ассео
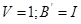
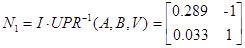
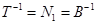
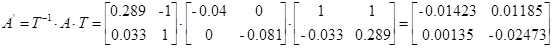
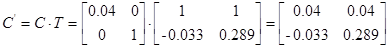
Внешне связное форму получаем из матрицы передаточных функций
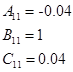
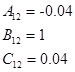
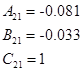
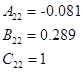
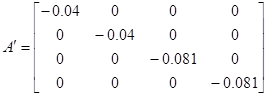
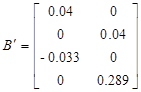
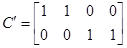
Вычисление МПФ системы
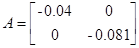
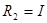 ;
; 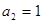 ;
; 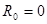 ; n=2; i=1;
; n=2; i=1; 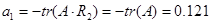
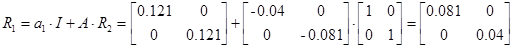
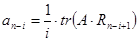
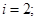
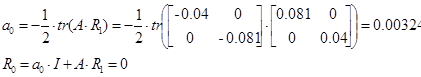
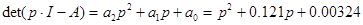
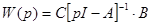
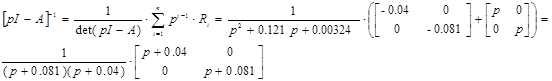
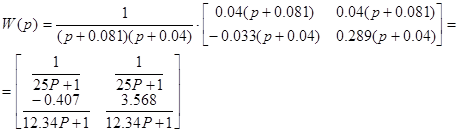
 2020-01-14
2020-01-14 133
133








