Для дискретной формы системы (F, G, C) из пункта 3. 1. провести реализацию системы.
Запишем систему в виде:
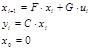
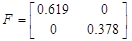
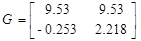
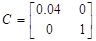
Подавая импульс по первому входу, рассчитаем:
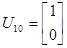
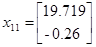
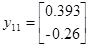
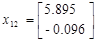
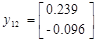
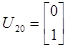
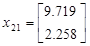
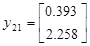
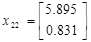
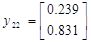
Теперь имея экспериментальные данные, сгруппировав их в матрицы H и H1 можем приступить к их обработки.
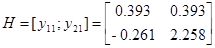
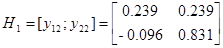
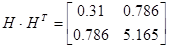
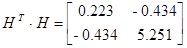
Из собственных векторов от (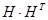 ) и (
) и (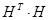 ) построим:
) построим:
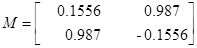
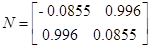
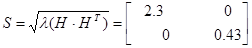
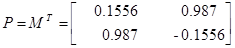
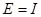
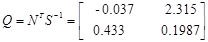
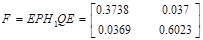
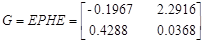
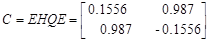
Для проверки идентификации найдем коэффициент передачи системы
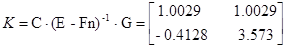
Коэффициент передачи, вычисленный по исходным матрицам
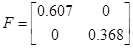
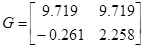
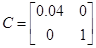
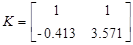
Можно сделать вывод о том, что система идентифицирована, верно
Пассивная идентификация
Для дискретной формы системы (F, G, C) из пункта 3. 1. провести пассивную идентификацию системы, предполагая, что вектор входа изменяется соответственно таблице:
Таблица 7 Значение вектора входа для пассивной идентификации.
| Такт, n | 0 | 1 | 2 | 3 | 4 | 5 |
| U(n) | 0.01 | 0 | 0 | 0.04 | 0 | 0 |
| 0 | 0.01 | 0.02 | 0 | 0.03 | 0 |
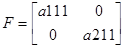
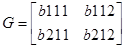
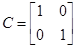
Используя матрицы системы в дискретной форме для заданных значений вектора входа, рассчитаем значения вектора выхода
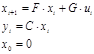
Результаты расчета сведем в таблицу:
| Такт, n | 1 | 2 | 3 | 4 | 5 | 6 |
| y(n) | 0.003935 | 0.006321 | 0.012 | 0.023 | 0.026 | 0.016 |
| -0.0026 | 0.022 | 0.053 | 0.0091 | 0.071 | 0.026 |
Используя данные эксперимента (Таблица 8) можем приступить непосредственно к определению параметров идентифицированной системы
Тогда
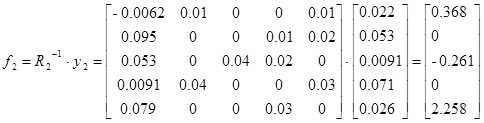
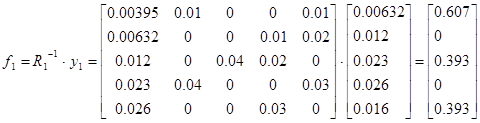
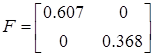
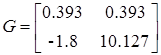
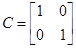
Для проверки идентификации найдем коэффициент передачи системы
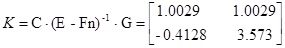
Система идентифицирована, верно
Конструирование многомерных регуляторов, оптимизирующих динамические свойства агрегата
Конструирование П. - регулятора, оптимизирующего систему по интегральному квадратичному критерию
Регулятор состояния, который оптимизирует систему по критерию:
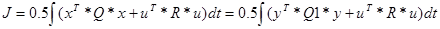

Определяется по соотношениям:
P=LR1(A,B,Q,R); 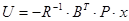

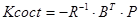 При этом Q=R=I
При этом Q=R=I
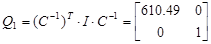
Т.к. матрица С. является инвертированной, для образования регулятора выхода нет необходимости конструировать наблюдатель состояния – недосягаемое состояние просто вычисляется по формуле 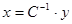 .
.
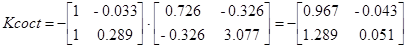
Следовательно, регулятор выхода имеет вид 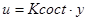
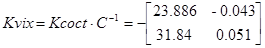
 2020-01-14
2020-01-14 96
96








