2020-01-14
316
Содержание
1. Расчет цилиндрической оболочки, подкрепленной шпангоутами
2. Исследование напряжённо-деформированного состояния полусферической оболочки, заполненной жидкостью
3. Исследование напряжённо-деформированного состояния сферической оболочки, заполненной жидкостью
4. Расчёт сферического топливного бака с опорой по экватору
5. Расчёт бака на прочность
Список литературы
РАСЧЕТ ЦИЛИНДРИЧЕСКОЙ ОБОЛОЧКИ, ПОДКРЕПЛЕННОЙ ШПАНГОУТАМИ
Условие задачи. Рассмотрим цилиндрическую оболочку постоянной толщины 
, радиуса 
, подкрепленную шпангоутами, равномерно расположенными по её длине. Сечение шпангоута: 
. Оболочка нагружена избыточным давлением 
(рис.1).
Цель расчета. Определить минимальное расстояние между шпангоутами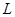 
, которое позволяет исключить взаимное влияние на оболочку двух соседних шпангоутов.
Рис.1. Расчетная схема
Исходные данные
Погонная нагрузка 
МПа;
Радиус оболочки 
м;
Толщина оболочки 
м;
Ширина шпангоута 
, м;
Толщина шпангоута 
, м;
Материал оболочки:
марка ВТ6С (О);
коэффициент Пуассона 
;
модуль Юнга 
Выполнение расчёта
Расчётная схема 1. Шпангоуты абсолютно жёсткие
Определим цилиндрическую жёсткость оболочки 
по формуле:
;
Вычислим коэффициент затухания 
гармонической функции 
по формуле:
;
Определим силу взаимодействия 
между шпангоутами и оболочкой:
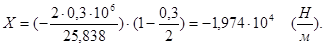
Определим перерезывающую силу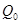 
на краю оболочки:
Определим погонный изгибающий момент 
в месте установки шпангоута:
Погонный изгибающий момент 
по длине оболочки, затухающий по периодическому закону, вычислим по следующей формуле:
где 
- число расчётных точек на всей области существования функции 
.
Принимаем 
.
Так как область существования гармонической функции определяется условием 
, то находим шаг вычислений 
момента из выражения:
;
Результаты расчёта заносим в таблицу 1 и вычерчиваем график функции 
(рис.2, рис.3).
С использованием графика определяем координату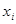 
второй точки пересечения графика функции 
с осью абсцисс и находим минимальное расстояние между шпангоутами 
:
