Рассмотрим участок оболочки  (рис. 1). На расстоянии
(рис. 1). На расстоянии  от полюса
от полюса 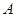 отсекаем часть оболочки нормальным коническим сечением с углом широты
отсекаем часть оболочки нормальным коническим сечением с углом широты  (рис. 2).
(рис. 2).
1.1 Определяем границы участка BC:  .
.
1.2 Составляем уравнение равновесия внешних и внутренних сил в проекции на вертикальную ось для отсечённой части оболочки:
 ,
,
где 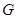 - вес жидкости, заполняющей полусферу;
- вес жидкости, заполняющей полусферу;  - координаты расчётного сечения;
- координаты расчётного сечения;  - меридиональная погонная сила.
- меридиональная погонная сила.

1.3 Определяем высоту столба жидкости в полусферической оболочке:

1.4 Находим объём шарового сегмента, заполненного жидкостью:
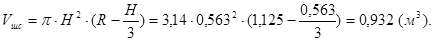
1.5 Вычисляем вес жидкости по формуле:

1.6 Определяем текущий радиус кольцевого сечения оболочки:

1.7 Находим погонное меридиональное усилие  из уравнения равновесия отсечённой части оболочки:
из уравнения равновесия отсечённой части оболочки:
 .
.
1.8 Определяем погонное кольцевое усилие 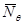 для участка
для участка 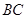 , используя уравнение Лапласа:
, используя уравнение Лапласа:
 ,
,
где  ,
, 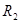 – главные радиусы кривизны расчётного сечения оболочки;
– главные радиусы кривизны расчётного сечения оболочки;
 – интенсивность внешней нагрузки на стенку в расчётном сечении оболочки.
– интенсивность внешней нагрузки на стенку в расчётном сечении оболочки.
Для сферы R1 = R2 и для участка 

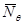 = -
= - 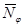 .
.
Результаты расчёта заносим в таблицу 1 при условии  .
.
Таблица 1
| № точки | 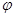 , град. , град.
| 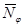 , Н/м , Н/м
|  , Н/м , Н/м
|
| 1 | 90 | 1035 | -1035 |
| 2 | 87 | 1037 | -1037 |
| 3 | 84 | 1046 | -1046 |
| 4 | 81 | 1061 | -1061 |
| 5 | 78 | 1081 | -1081 |
| 6 | 75 | 1109 | -1109 |
| 7 | 72 | 1144 | -1144 |
| 8 | 69 | 1187 | -1187 |
| 9 | 66 | 1240 | -1240 |
| 10 | 63 | 1303 | -1303 |
| 11 | 60 | 1380 | -1380 |
 2020-01-14
2020-01-14 162
162








