2020-01-14
288
Рис. 3. Сечение II – II
Нормальным сечением к оси бака II – II отсечём часть цилиндра, расположенную над зеркалом жидкости (рис. 3). Составим уравнение равновесия для верхней отсеченной части оболочки в проекции на вертикальную ось:
.
Отсюда меридиональное напряжение:
Па.
Для цилиндра 
; 
, поэтому из уравнения Лапласа получаем кольцевое напряжение:
Па.
Участок цилиндра под зеркалом жидкости
Рис. 4. Сечение III – III
Для сечения III – III расчётная схема (рис. 4) будет отличаться от показанной на рис. 3 тем, что здесь необходимо дополнительно учесть давление на стенку цилиндрической части бака со стороны жидкости.
Уравнение равновесия в проекции на вертикальную ось бака остаётся без изменений:
.
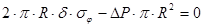Поэтому меридиональное напряжение не меняется:
Па.
Окружное напряжение определяем из уравнения Лапласа
,
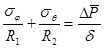где 
Па.
Отсюда 
Па.
Участок нижнего полусферического днища
Рис. 5. Сечение IV – IV
Для нижнего днища нормальным коническим сечением IV – IV с углом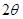 
при вершине отсечём нижнюю часть сферической оболочки (рис. 5). Составим для неё уравнение равновесия внешних и внутренних сил в проекции на вертикальную ось оболочки:
,
где r – радиус кольцевого сечения оболочки, 
;
S – площадь поперечного сечения, 
;
- давление в расчётном сечении оболочки, 
;
G – вес жидкости в объёме шарового сегмента, 
;
Vc – объём шарового сегмента, 
.
Подставляя значения r, S, 
, G в уравнение равновесия определяем меридиональное напряжение 
:
Уравнение Лапласа для сферической оболочки имеет вид:
.
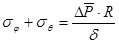Подставляя в уравнение Лапласа 
, находим кольцевое напряжение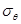 
в сечении IV – IV:
.
Построим таблицу 2 значени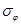й 
и 
в зависимости от угла 
в диапазоне от 0˚ до 90˚ с шагом в 15˚:
Таблица 2
 , град
| , МПа
|  , МПа
|
| 0 | 
| 
|
| 15 | 
| 
|
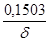
| 30 | 
| 
|
| 45 | 
| 
|
| 60 | 
| 
|
| 75 | 
| 
|
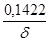
| 90 | 
| 
|
По полученным напряжениям в характерных сечениях бака строим эпюры напряжений 
и 
(рис. 6).
