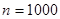Определение оценок параметров распределений

Метод моментов

Метод моментов заключается в том, что определенное количество статистических начальных и (или) центральных моментов приравнивается к соответствующим теоретическим моментам распределения случайной величины. Уравнения метода показано в формуле (2.23).

 

(2.23)

 

(2.24)

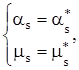
где  – теоретический начальный момент 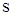-того порядка для непрерывной случайной величины, вычисляется по формуле (2.24):

 

.

 

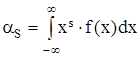 – статистическая оценка соответствующего теоретического момента 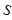-того порядка, вычисляется по формуле (2.25):

 

(2.25)

.

 

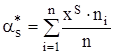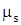 – теоретический центральный момент s-того порядка, вычисляется по формуле (2.26):

(2.26)

.

 

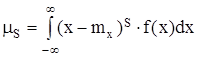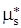 – статистическая оценка теоретического центрального момента 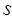-того порядка, вычисляется по формуле (2.27):

 

(2.27)

.

 

Из системы (2.23) находятся параметры распределения. Число уравнений в системе зависит от количества неизвестных параметров. Для нормального и равномерного законов, система должна содержать два уравнения, для экспоненциального – одно.

Для равномерного закона распределения система (2.23) принимает вид (2.28):

 

(2.28)

 

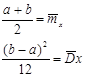
Из системы 2.28 нужно найти параметры 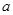 и .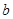

В таблице 2.38 приведены значения этих параметров, найденные методом моментов и методом максимального правдоподобия.

 

Таблица 2.38 – Значения параметров 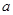 и

	(метод моментов)	(метод максимального правдоподобия)	∆	(метод моментов)	(метод максимального правдоподобия)	∆
	6,993	6,996	0,003	25,201	25,542	0,341
	6,984	7,313	0,329	25,110	25,065	0,045
	6,711	6,849	0,138	25,237	25,051	0,186

Из таблицы видно, что значения параметров, найденные разными методами, практически совпадают. Это подтверждает, что случайная величина 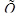 распределена по равномерному закону.

Метод максимального правдоподобия

По методу максимального правдоподобия, строится так называемая функция правдоподобия (2.29):

 

(2.29)

 

где 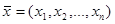 – выборка,

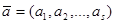 – вектор параметров.

Необходимо найти такие значения вектора 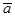, чтобы функция  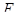достигала максимума. Для этого строят систему правдоподобия (2.30), содержащую частные производные от функции правдоподобия по всем переменным, приравненные к нулю. Для упрощения вычислений переходят к функции 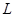, равной логарифму натуральному от :

 

(2.30)

 .

 

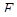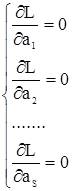Оценки параметров, получаемые из этой системы, называют оценками максимального правдоподобия.

Для равномерного закона функция правдоподобия будет иметь вид (2.31)

(2.31)

 

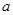где  и 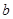 – параметры распределения.

Данная функция будет достигать максимума при условии (2.32):

 

 

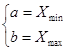
Судя по полученным оценкам параметров распределения, можно сделать вывод, что наше предположение было верно изначально и случайная величина  действительно распределена равномерно.