2020-04-07
2762
Резистора, катушки и конденсатора
Построение диаграммы начнем с вектора напряжения, которое одинаково для всех элементов цепи и предопределяет их токи, положим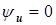 
. Ток резистора также имеет нулевую начальную фазу, векторы 
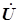и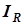 
коллинеарны (рис. 4.14).
| 
|
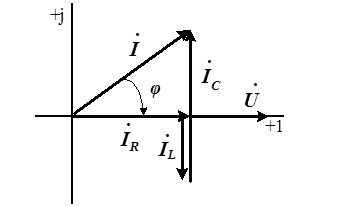Рис. 4.14. Векторная диаграмма токов и напряжения для цепи с параллельным
включением элементов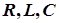 
(
)
Векторы токов в реактивных элементах 
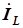и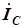 
перпендикулярны вектору напряжения. Вектор 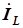отстает от вектора 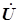на 
. Вектор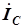 
опережает вектор напряжения на 
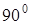. Векторы токов 
, 
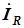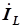и 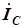нанесены на диаграмму в порядке расположения соответствующих элементов в цепи. Начало каждого последующего вектора совмещено с концом предыдущего вектора, чтобы упростить суммирование трех векторов токов.
Согласно первому закону Кирхгофа
,
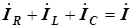где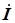 
- входной комплексный ток. Векторы токов в элементах цепи просуммированы на диаграмме по правилу многоугольника. Угол сдвига фаз между напряжением и током в данном случае оказался отрицательным, рассматриваемая цепь имеет емкостный характер (в параллельных ветвях 
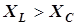и соответственно 
).
|
|
|
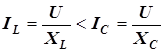Векторная диаграмма цепи со смешанным соединением
Элементов
Построение векторной диаграммы токов и напряжений для цепи, показанной на рис. 4.15, начнем с вектора напряжения на параллельных элементах, которому припишем нулевую начальную фазу (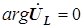
, 
).
| 
|
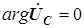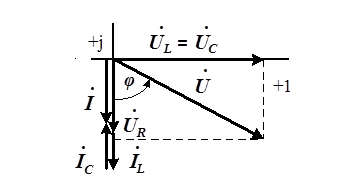Рис. 4.15. Векторная диаграмма токов и напряжений со смешанным соединением
элементов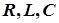 
(
)
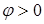Векторы токов в реактивных элементах перпендикулярны вектору напряжения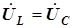 
. Вектор 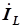отстает от вектора 
на 
. Вектор 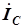опережает вектор 
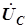на 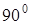. Входной ток определен по первому закону Кирхгофа
;
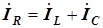суммирование векторов выполнено по правилу многоугольника (который выродился в прямую и слился с осью мнимых). Напряжение на резисторе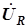 
имеет такой же аргумент, как и входной ток 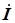, векторы 
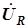и 
коллинеарны. Входное напряжение определено по второму закону Кирхгофа
;
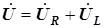сложение векторов выполнено по правилу параллелограмма. Угол между входным напряжением и током оказался положительным. Рассматриваемая цепь имеет индуктивный характер (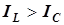
, 
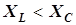в параллельных ветвях).
Если комплексным напряжениям и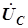 
, с которых начато построение диаграммы, приписать не нулевые аргументы, а принять 
, то есть направить векторы и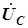 
по оси мнимых, то векторная диаграмма на рис. 4.15 переместится из четвертого квадранта комплексной плоскости в первый квадрант. Все векторы вслед за и 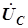повернутся против часовой стрелки на .
