Метод прямоугольников

Разбиение интервала интегрирования  на n частей приводит к возможности рассмотрения площадей криволинейных трапеций на каждом небольшом отрезке . Учитывая малую величину шага разбиения , площадь такой фигуры можно считать приближенно равной площади прямоугольника со сторонами  и h (рис.20).

Рис.20.  Графическая интерпретация метода прямоугольников

Y 0

0 x 0 =a x 1 x 2…. xixi +1…                        xn=b

Y 1

Y=F (x)

X

Y

Y 2

Yi

Yi+ 1

Yn

 

 

Суммирование значений таких площадей позволяет получить формулу "левых" прямоугольников

Метод трапеций

Замена интеграла

на каждом элементарном участке площадью трапеции с основаниями
 и высотой h  приводит после суммирования к следующей формуле

 

Метод Симпсона (парабол)

Разбиение промежутка  на четное число  отрезков позволяет на каждой паре отрезков  заменить подынтегральную функцию параболой .

Площадь фигуры, ограниченной сверху параболой, считается по формуле

Суммирование таких интегралов (площадей, ограниченных параболами)

приводит к более точной, чем предыдущие, формуле

 

Решение

1. Оформите лист Excel следующим образом (рис. 21):

 

	A	B	C	D	E	F	G
1
2	Вычислить интеграл  при a = 0 и b = 1.
3	a	b	h	m	Методы:
4	0	1	0,0625	16	прямоугольников	трапеций	Симпсона
5		x	f(x)
6		0	1
7		0,125	0,06066
…
22		1	1,73205

 

Рис. 21. Шапка таблицы

2. Введите формулы:

в ячейку С4:  = (B4– A4)/D4;

         в ячейку В6: =А4;

         в ячейку С6: =КОРЕНЬ(2*В6+1),

определяющие значение подынтегральной функции.

3. Введите формулу

в ячейку B7: =В6+$C$4.

 Затем заполните столбец В с помощью маркера автозаполнения.

4. Затем выделите ячейку С6, и проделайте то же самое в столбце С.

 

 

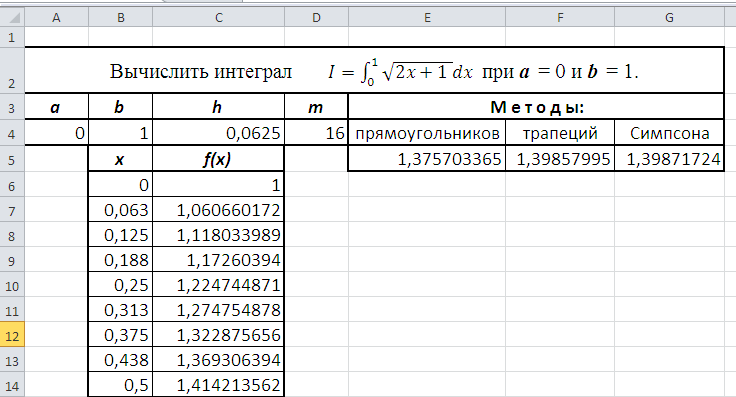
Рис. 22. Результаты вычисления интеграла различными способами

 

5. В ячейки E5, F5 и G5 введите следующие формулы:

E5: = C4*CУММ (С6:С22);

F5: = C4*((C6+C22)/2+CУММ (С6:С21);

G5: = C4/3*((C6+4*(C7+C9+C11+C13+C15+C17+C19+C21)+

2*(С8+c10+c12+c14+c16+c18+c20)+c22).

Результаты вычисления интеграла представлены на рис. 22.

Лабораторная работа №12

Нахождение корней нелинейного уравнения

Задание

Определить все корни уравнения

при a = 1; b = – 5,5; c = – 50; p = 112,5.