Лабораторная работа № 4

ИССЛЕДОВАЯИЕ САУ СКОРОСТЬЮ ДВИГАТЕЛЯ, СИНТЕЗИРОВАННОЙ МЕТОДОМ ПОСЛЕДОВАТЕЛЬНОЙ ОПТИМИЗАЦИИ КОНТУРОВ

4.I. Цель работы

Изучение метода последовательной оптимизации контуров. 

4.2. Последовательность синтеза САУ методом

последовательной оптимизации контуров

ЗИ

Wpc

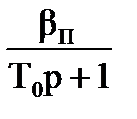
Wpт

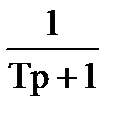
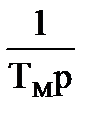
КТ

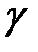
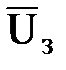
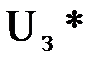
ЗИ

Wpc

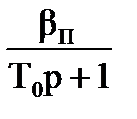
Wpт

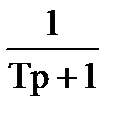
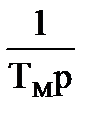
КТ

Структурная схема астатической САУ подчинённого регулирования скоростью электродвигателя представлена на рис. 4.1. На этом рисунке приняты обозначения: Т_м и Т - соответственно электромеханическая и электромагнитная постоянные времени: Т₀ и β_п - постоянная времени и коэффициент усиления вентильного преобразователя; k_т и ɣ - коэффициенты обратной связи по току и э. д. с. электродвигателя; W_рт и W_рс - передаточные функции соответственно регулятора тока и скорости; ЗИ - задатчик интенсивности, необходимый для формирования требуемых динамических характеристик по задающему воздействию.

 

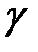
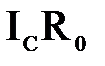
(4.1)

Сущность метода синтеза заключается в том, что вначале синтезируется контур тока, а затем контур скорости. Причём оба контура синтезируются из условия максимального быстродействия, что позволяет более качественно отработать закон изменения задающего воздействия U_з.

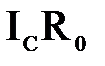
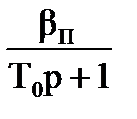
Wpт

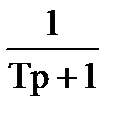
КТ

 Структурная схема контура регулирования тока без учёта внутренней отрицательной обратной связи по э. д. с. двигателя имеет вид:

 

(4.2)

 

 Здесь U_зт – направление задания тока. I – ток электродвигателя.

Приняв передаточную функцию регулятора тока:

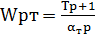                                                                                                  (4.1)

Из рисунка (4.2) можно записать:
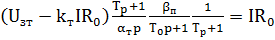                                                    (4.2)

Из (4.2) следует, что передаточная функция контура тока имеет вид:
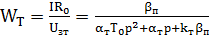                                                            (4.3)

Целью синтеза контура тока является определение постоянной времени α_Т пропорционально-интегрального регулятора тока. Характеристическое уравнение контура тока имеет вид:

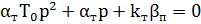
Примем корим характеристического уравнения, соответствующие техническому оптимуму:

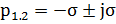
Согласно теореме Виетта характеристическое уравнение можно представить:   

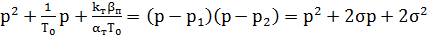(4.4)

Приравняв коэффициенты при одинаковых степенях равенства (4.4) получим:

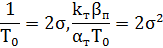
Таким образом

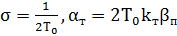                                                                        (4.5)

С учетом (4.5) передаточная функция контура тока имеет вид:

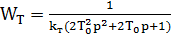                                                                         (4.6)

Структурная схема контура регулирования скорости с учетом (4.6) представлена на рис. 4.3.

Из рис. 4.3 можно записать:

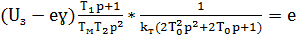                                                (4.7)

Из 4.7 следует, что передаточная функция контура регулирования э. д. с. (скорости) двигателя будет иметь вид:

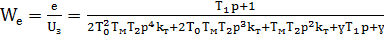 (4.8)

    Целью синтеза контура скорости является определение параметров пропорционально-интегрального регулятора скорости Т₁ и Т₂ .

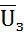
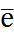
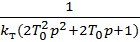
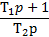
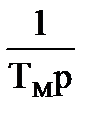
ɣ

 

                                          Рис. 4.3

Зададимся корнями характеристического уравнения передаточной функции (4.8) 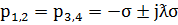                                                   (4.9)

Согласно теореме Виетта с учетом (4.8) и (4.9) можно записать равенство:

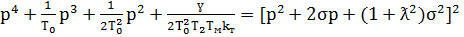                      (4.10)

Вводя обозначения:

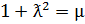                                                                                           (4.11)

И приравнивая коэффициенты при одинаковых степенях равенства (4.10) получим:

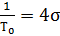                                                                                                         (4.12)

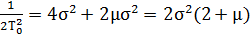                                               (4.13)

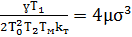                                                                                 (4.14)

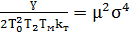                                                                            (4.15)

Из (4.12) и (4.13) следует:

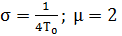                                                                                             (4.16)

Из (4.14) и (4.15) можно определить Т₁ и Т_2.

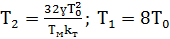                                                                         (4.17)

Корни характеристического уравнения контура регулирования скорости будут иметь вид:

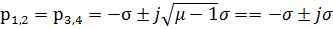
4.3 Схема модулирования САУ

Схема модулирования представлена на рисунке 4.4

Здесь:

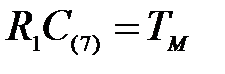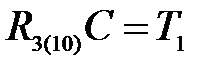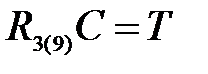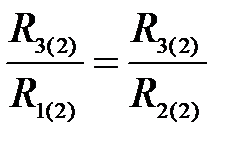; ; ; ; =1; ;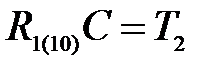 

; ; ; 

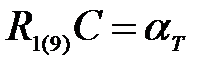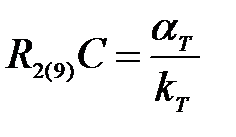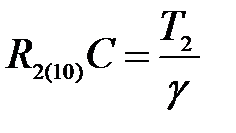Приведенные соотношения позволяют определить положения программных переключателей.

4.4 Исходные данные к работе

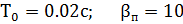; ɣ=1      

 

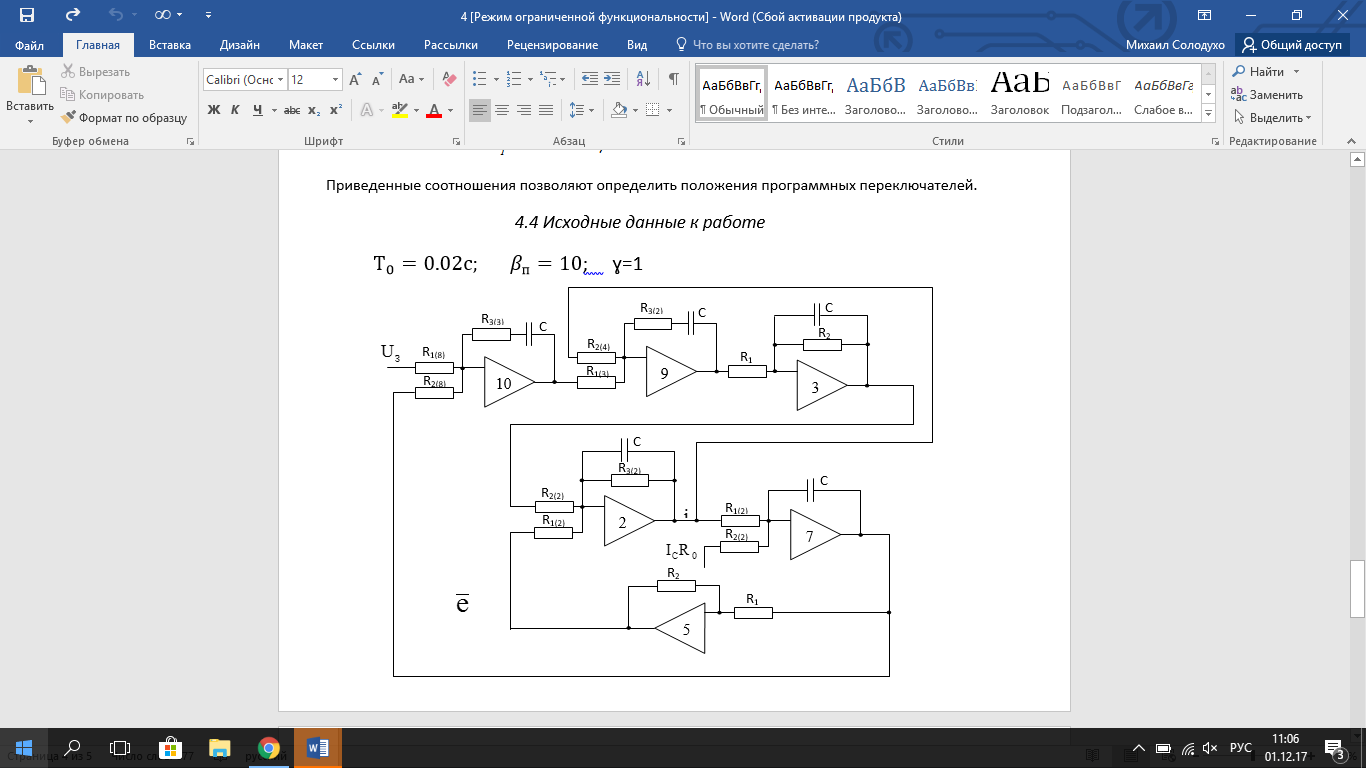
Вариант	1	2	3	4	5	6	7	8	9	10	11	12
	0,02	0,04	0,08	0,12	0,15	0,02	0,04	0,08	0,12	0,04	0,08	0,12
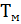
	0,05	0,06	0,08	0,2	0,25	0,06	0,15	0,06	0,12	0,05	0,06	0,06
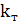
	0,5	0,5	0,5	1	1	1	0,25	0,5	0,5	1	1	0,5

4.4 Порядок выполнения работы

       1. В соответствии с исходными данными табл. 4.1 необходимо

рассчитать параметры регулятора скорости и тока.

       2. Вычертить схемы моделировании САУ и указать положение

программных переключателей.

       3. Снять осциллограммы переходных процессов для скорости и

тока электродвигателя по возмущающему воздействию и задающему

без задатчика интенсивности.

       4. Снять осциллограммы переходных процессов для скорости и

тока электродвигателя по задающему воздействию с задатчиком интенсивности (два значения времени пуска двигателя 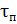 задаются

преподавателем).

       5. Снять осциллограммы переходных процессов без обратнойсвязи по току.4.6. Содержание отчёта       1. Название и цель работы.       2. Структурная схема САУ и расчёт параметров регулятора токаи регулятора скорости.       3. Схемы моделирования САУ с аадатчиком интенсивности и беззадатчика.       4: Построить осциллограммы переходных процессов по задающему и возмущающему воздействию.4.7. Контрольные вопросы       1. Как рассчитать контур регулирования тока?       2. Как рассчитать контур регулирования скорости?       3. Как рассчитать переходные процессы для тока и скоростипри наличии задатчика интенсивности?       4. Назначение задатчика интенсивности.       5. Уметь пояснить графини переходных процессов для тока искорости электродвигателя по задавшему и возмущающему воздействию.