Лабораторная работа №8

ИССЛЕДОВАНИЕ НАБЛЮДАТЕЛЯ ДЛЯ ИЗМЕРЕНИЯ ВЕКТОРА СОСТОЯНИЯ САУ

8.1. Цель работы

Изучить метод синтеза наблюдателей для измерения вектора со­стояния САУ и экспериментально исследовать показатели качества работы разомкнутого и замкнутого наблюдателей.

8.2. Основные понятия и определения

Пусть объект управления описывается уравнением состояния, записанным в матричном виде:

                                                                                      (8.1)

 ,                                                                                                 (8.2)

где X и U - это соответственно вектор состояния объекта управления и вектор управления; А и B - матрицы; У - вектор изме­ренных координат объекта управления.

В теории управления существует понятие управляемости и наблюдаемости САУ /3/. Причем, если объект является управляемым и наблюдаемым, то он является и идентифицируемым. То есть, по входному сигналу U и измеренному значению Y можно восстановить вектор состояния объекта управления X. Условие управляемости и наблюдаемости имеет вид

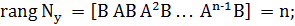                                              (8.3)

                                       (8.4)

To есть, ранг матрицы управляемости 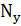 и наблюдаемости  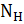дол­жен быть равен порядку дифференциального уравнения (n), описываю­щего поведение объекта.   . *

Наблюдатели или идентификаторы могут быть разомкнутыми или замкнутыми. Алгоритм работы разомкнутого наблюдателя имеет вид

/3/:                                                                                (8.5)

 ,                                                                              (8.6)

Здесь 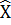 и - соответственно оценочное значение вектора состоя­ния объекта управления и вектор выходных координат наблюдателя.

Ввиду несовпадения начальных условии объекта управления и наблюдателя, то есть  , а также изменений коэффициентов матрицы А или неточного определения на этапе проектирования, та­кой наблюдатель обладает невысокой точностью измерения и на прак­тике широкого распространения не получил. На практике распростра­нение получили замкнутые наблюдатели, алгоритм функционирования которых имеет вид:

                                                                      (8.7)

Структурная схема наблюдателя представлена на рис. 8.1.

 

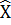
Уравнение (8.7) с учетом (8.2) примет вид

                                                    (8.8)

Собственные значения матрицы

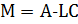                                                                                  (8.9)

будут определять быстродействие наблюдателя. Обычно быстродействие наблюдателя принимают в несколько раз выше быстродействия САУ, которая замыкается через наблюдатель.

Целью синтеза наблюдателя является определение коэффициентов матрицы L исходя из его быстродействия. Указанные коэффициенты можно определить методом теории модального управления. Структур­ная схема исследуемого объекта управления представлена на рис. 8.2.

 

 

 

Необходимо синтезировать наблюдатель для измерения недостаю­щих координат  и  по информации о входном воздействии U и выходном х=у. Уравнения состояния объекта управления имеют вид

Из (8.10) следует, что

Здесь ;

Матрица L имеет вид

С учётом (8.14) и (8.11) запишем

 (8.15)

 учётом (8.15) выражение (8.9) примет вид

Собственные значения матрицы М определяются из выражения

 (8.17)

где Е - единичная матрица; λ - собственные значения матрицы. Раскрывая выражение (8.17). получим

 

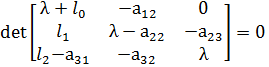
C учётом (8.12), (8.13) выражение (8.18) примет вид

 

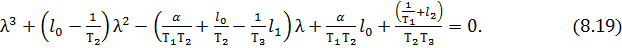
Зададимся распределением собственных значений матрицы М по Бат- терворту

Здесь n=3.

Расположение собственных значений  показано на рис. 8.3. Согласно теореме Виетта выражение (8.19) можно представить

C учётом рис. 8.3

 (8.22)

Причём  

.

Модуль собственного значения Н определяет быстродействие наблюдателя /2/

где время регулирования.

 

 

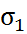
С учётом (8.22) выражение (8.21) примет вид

              (8.25)

Приравнивая коэффициенты при одинаковых степенях 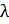 выраже­ний (8.19) и (8.25), получим три уравнения для нахождения  ,  и :

 (8.26)

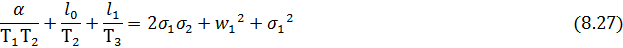
Таким образом, методика синтеза заключается в следующем. По быстродействию наблюдателя из (8.24) определяется Н, затем по (8.23) находятся значения , ,  и по (8.26)-(8.28) опре­деляются значения ,  и .

8.3. Схема моделирования объекта совместно с наблюдателем

Раскрывая уравнение (8.7) с учетом (8.11) и (8.14), запишем уравнения состояния замкнутого наблюдателя:

                                                 (8.30)

В разомкнутом наблюдателе

Уравнения состояния объекта имеют вид

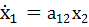
                                                                                    (8.31)

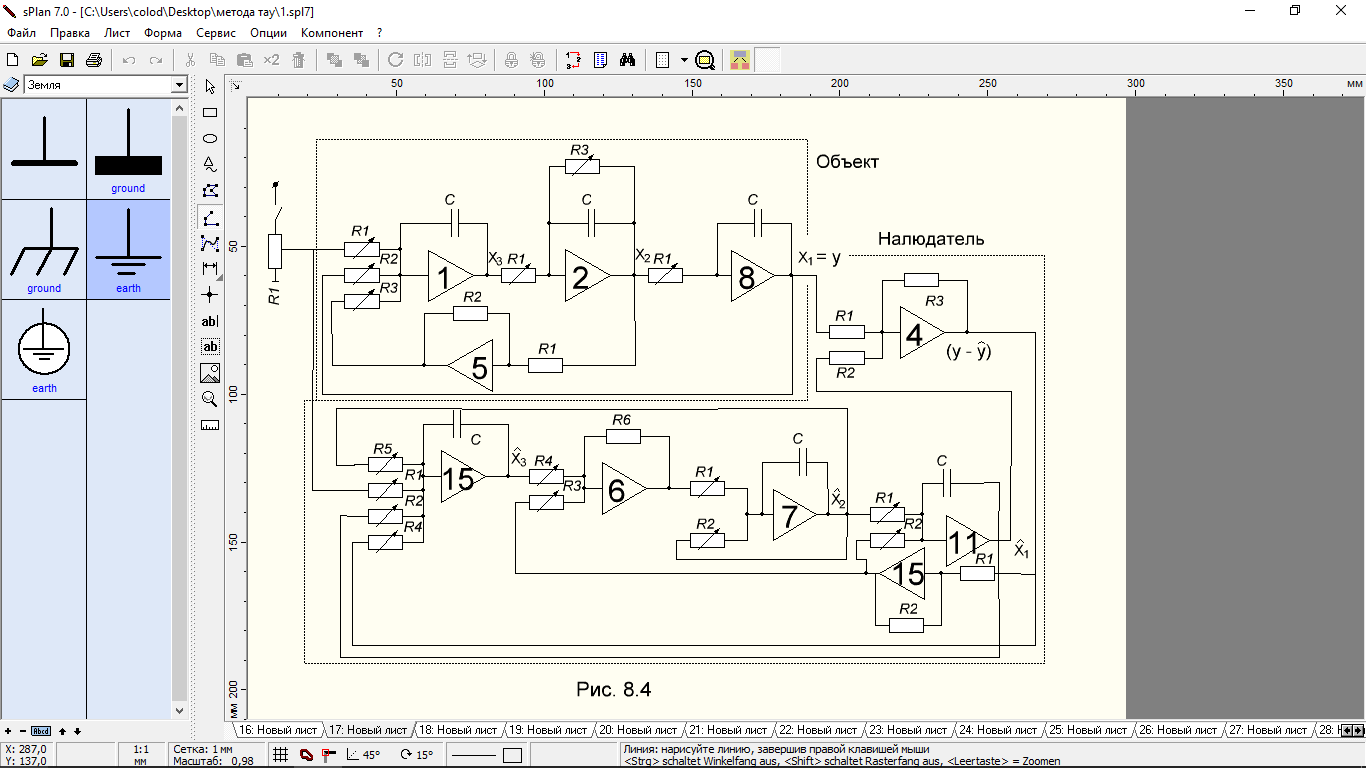
Схема моделирования объекта совместно с наблюдателем (замкнутым) имеет вид, представленный на рис. 8.4.

Положения программных переключателей могут быть определены из следующих соотношений:

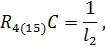
В скобках указан номер операционного усилителя.

8.4. Исходные данные к работе

Таблица 8.1

Характеристика	1	2	3	4	5	6	7	8	9
	0.2	0.22	0.25	0.18	0.25	0.3	0.25	0.3	0.27
	0.1	0.2	0.25	0.1	0.2	0.25	0.1	0.2	0.1
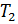
	0.15	0.88	0.12	0.08	0.15	0.2	0.06	0.12	0.15
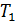
	0.2	0.2	0.1	0.1	0.1	0.05	0.1	0.05	0.2
α	2	1	1	2	2	2	2	1	1

 

8.5. Порядок выполнения работы

1. В соответствии с исходными данными табл. 8.1 осуществить синтез наблюдателя для измерения вектора состояния объекта управ­ления.

2. Вычертить схему моделирования объекта управления совмест­но с наблюдателем с указанием положений программных переключате­лей.

3. При ступенчатом изменении снять осциллограммы изменения координат объекта управления  ,  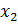,  и осциллограммы изме­нения измеренных координат наблюдателем  ,  , для следу­ющих вариантов:

а) наблюдатель разомкнут (выход усилителя 4 не подключается к наблюдателю);

б) наблюдатель замкнут.

Пункты а) и б) выполняются для случая отклонения параметров объекта от заданных (отклонения 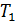, , 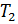 задаются преподава­телем).

4. Пункты I и 2 выполняются в ходе домашней подготовки к выполнению работы.

8.6. Содержание отчёта

1. Название и цель работы.

2. Синтез наблюдателя.

3. Структурная схема наблюдателя совместно с объектом уп­равления.

4. Схема моделирования наблюдателя совместно с объектом управления с указанием положений программных переключателей.

5. Для всех случаев, указанных в пункте 3, построить осцил­лограммы изменения координат объекту управления и координат, из­меренных наблюдателем.

8.7. Контрольные вопросы

1. Понятие управляемости и наблюдаемости САУ.

2. Идентифицируемость объекта управления.

3. Назначение наблюдателей. Разомкнутые и замкнутые наблюдатели.

4. Методика синтеза замкнутых наблюдателей.

5. Недостатки разомкнутых наблюдателей.