Задача 51. Вычислить массу шара радиуса 1, если плотность равна квадрату расстояния от центра шара.
Решение. Функция  , это равно
, это равно  , так как
, так как
 . Кроме этого, умножим на определитель Якоби сферических координат, то есть
. Кроме этого, умножим на определитель Якоби сферических координат, то есть  .
.
Радиус равен 1, так что очевидно,  .
.
 ,
,  ,
,  .
.
Итак,  =
=  =
=
 =
=  =
=  =
=
 =
=  . Ответ.
. Ответ.  .
.
Задача 52. Вычислить тройной интеграл с помощью сферических координат: 
Решение. Чтобы перейти к новым координатам, рассмотрим, по какому трёхмерному телу ведётся интегрирование. Уравнение линии, которой достигает точка по  , имеет вид
, имеет вид  , что сводится к
, что сводится к  , то есть это окружность радиуса 1. Таким образом, при
, то есть это окружность радиуса 1. Таким образом, при 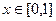 движемся вверх по
движемся вверх по  до окружности, то есть основание фигуры это четверть круга. Теперь рассмотрим, до куда точка движется по
до окружности, то есть основание фигуры это четверть круга. Теперь рассмотрим, до куда точка движется по  , в условии указано, что
, в условии указано, что  от 0 до
от 0 до  . Но уравнение
. Но уравнение  сводится к
сводится к  , т.е. это сфера радиуса 1. Таким образом, область интегрирования это 1/8 шара единичного радиуса в первом октанте, т.е. в той части пространства, где
, т.е. это сфера радиуса 1. Таким образом, область интегрирования это 1/8 шара единичного радиуса в первом октанте, т.е. в той части пространства, где  .
.
Пределы интегрирования таковы:  ,
,  ,
, 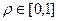 .
.
Пересчитаем подынтегральную функцию, чтобы выразить её через  . В данном случае видим корень из суммы квадратов всех координат, поэтому сразу можно заметить, что по теореме Пифагора
. В данном случае видим корень из суммы квадратов всех координат, поэтому сразу можно заметить, что по теореме Пифагора  . Кроме того, умножим на определитель Якоби сферических координат, то есть
. Кроме того, умножим на определитель Якоби сферических координат, то есть  .
.
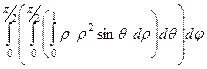 =
=  =
=
 =
=  =
= 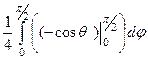 =
=  =
= 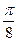 .
.
Ответ.  .
.
Задача 53. Вычислить тройной интеграл по 1/8 части шара в 1-м октанте от функции  .
.
Решение. Трёхмерное тело такое же, как в прошлой задаче. Значит, границы те же самые. В функции надо будет выразить всё через  по формулам сферических координат.
по формулам сферических координат.

 =
=
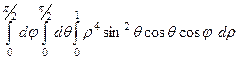 далее, мы видим, что все множители зависят только от различных переменных, поэтому можно вынести их в соответствующий интеграл и считать не как вложенные действия, а как произведение.
далее, мы видим, что все множители зависят только от различных переменных, поэтому можно вынести их в соответствующий интеграл и считать не как вложенные действия, а как произведение.
 . Здесь в первом интеграле -
. Здесь в первом интеграле -  =
=
 =
= 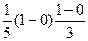 =
=  Ответ.
Ответ.  .
.
Задача 54. Найти объём тела, ограниченного конусом
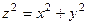 и сферой радиуса
и сферой радиуса  .
.
Решение. Чертёж:

Конус пересекается со сферой радиуса  на высоте
на высоте  .
.
Отклоенние угла  достигает от 0 до 45 град, чтобы пересечение луча с фигурой существовало. Любой отрезок, проведённый из начала координат (если он упирается в сферу, находится внутри этой фигуры) имеет длину
достигает от 0 до 45 град, чтобы пересечение луча с фигурой существовало. Любой отрезок, проведённый из начала координат (если он упирается в сферу, находится внутри этой фигуры) имеет длину  . Итак,
. Итак,
 =
=  =
=
 =
=  =
= 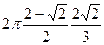 =
=
 =
=  .
.
Ответ.  .
.
Задача 55. Вычислить объём тела, ограниченного цилиндром  и двумя плоскостями
и двумя плоскостями  в цилиндрических координатах.
в цилиндрических координатах.

Решение. На чертеже показано строение фигуры: 2 среза из цилиндра, один с помощью горизонтальной плоскости  , другой с помощью наклонной плоскости
, другой с помощью наклонной плоскости  . Зелёным закрашено основание этой фигуры, а именно, полукруг в правой полуплоскости.
. Зелёным закрашено основание этой фигуры, а именно, полукруг в правой полуплоскости.
Для того, чтобы точка в плоскости находилась в основании этой фигуры, требуется  ,
,  . Определим теперь границы последнего из вложенных интегралов, самого внутреннего, который по переменной
. Определим теперь границы последнего из вложенных интегралов, самого внутреннего, который по переменной 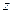 . Если
. Если  , от горизонтальной до наклонной плоскости. При этом,
, от горизонтальной до наклонной плоскости. При этом, 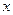 нужно выразить в цилиндрических координатах, ведь границы интегрирования внутреннего интеграла должны зависеть от внешних переменных
нужно выразить в цилиндрических координатах, ведь границы интегрирования внутреннего интеграла должны зависеть от внешних переменных  . Поэтому
. Поэтому 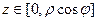 . Функция тождественная 1, чтобы вычислить объём, но при этом не забываем домножить на якобиан цилиндрических координат, то есть на
. Функция тождественная 1, чтобы вычислить объём, но при этом не забываем домножить на якобиан цилиндрических координат, то есть на  . Итак, получается
. Итак, получается  .
.
Вычислим этот интеграл. Сначала в самом внутреннем из них применяется формула Ньютона-Лейбница по переменной 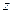 .
.
 =
= 
Теперь уже остался не тройной, а двойной интеграл. Во внутренней скобке применяется формула Ньютона-Лейбница по  .
.
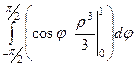 =
=  =
=  =
=  .
.
Ответ. 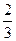 .
.
 2020-04-07
2020-04-07 155
155








