2020-04-07
116
Задача 47. Вычислить 
по кубу 
.
Решение. 
. Здесь уже 3 а не 2 вложенных цикла.
Это также можно записать в виде: 
.
Сначала вычислим внутренний интеграл по 
и применим формулу Ньютона-Лейбница именно к переменной , остальные при этом вычислении остаются в роли параметров, вместо них ничего не подставляется.
= 
.
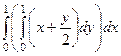Теперь первообразная по 
и формула Ньютона-Лейбница применяется в этой скобке именно к 
.
= 
. А теперь уже обычный определённый интеграл. 
= 
= 
.
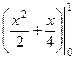Ответ. 
.
Задача 48. Вычислить тройной интеграл 
.
Решение. 
= 
= 
=
= 
= 
= 
.
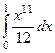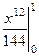Ответ. .
Задача 49. Найти объём тела, ограниченного поверхностями: 
.
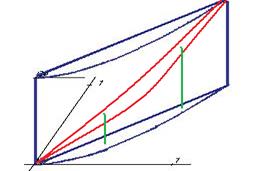
Решение. Метод построения 3-мерного чертежа: сначала выбрать все те уравнения, которые не содержат , и построить плоскую проекцию (вид сверху) этой фигуры. Строим графики 
.
Теперь видно, что 
, а при каждом фиксированном 
, 
.
Вообще, 
в плоскости это - уравнения кривых, но для пространства это уравнения поверхностей. Отсутствие 
означает, что любое, то есть к прямой и параболе присоединены вертикальные образующие. Представьте, что один вертикально поставленный лист ровный, а второй изогнут по параболе. Внутри такой узкой «шахты» как раз и располагается искомая фигура.
А теперь определим границы по высоте, чтобы окончательно построить чертёж. Для каждой точки, взятой на плоскости в том основании, которое показано на предыдущем чертеже, высота меняется от 
до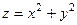 
, эти линии отмечены зелёным цветом. Эллиптический параболоид пересекается с каждой из указанных ранее вертикальных стенок, пересечения показаны красным цветом.
Самая верхняя точка (1,1,2). Итак, изобразим каркас этой фигуры:
Так как вычисляется объём, то надо полагать 
.
= 
= 
=
= 
= 
= 
= 
= 
= 
= 
.
Ответ. 
.
Задача 50. Найти объём тела, ограниченного поверхностями
.
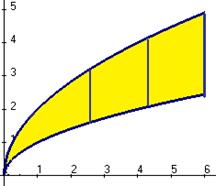
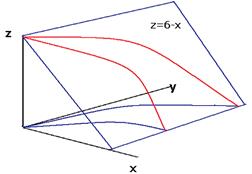
Решение. Построим плоский чертёж (вид сверху) рассматривая только те уравнения, которые не содержат . Это позволит записать внешние интегралы по 
. Третий, внутренний, который по 
, в пределах от 0 до 
.
= 
= 
=
= 
= 
=
= 
= 
=
= 
= 
= 
= 
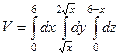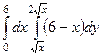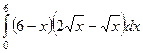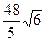. Ответ. 
.
