Томский государственный университет систем управления и радиоэлектроники
Приходовский М.А.
Математика
Курс практических занятий
Семестр 2
Учебное пособие
Для специальностей
Информатика и вычислительная техника»
Инфокоммуникационные технологии и системы связи»
Радиоэлектронные системы и комплексы»
Томск
ТУСУР
2020
Электронное учебное пособие составлено по материалам практических занятий в группах 589-1,2,3, 129, 1В9 весной 2020 года.
Пособие может представлять методический интерес для преподавателей, работающих на аналогичных специальностях, как материал для планирования занятий.
Оглавление
Определённый интеграл...................................................................................... 5
Приложения определённого интеграла............................................................ 10
Несобственный интеграл................................................................................... 17
Двойной интеграл в декартовых координатах................................................. 25
|
|
|
Двойной интеграл в полярных координатах.................................................... 32
Тройной интеграл в декартовых координатах................................................. 36
Тройной интеграл в цилиндрических и сферических координатах.............. 40
Криволинейные интегралы.............................................................................. 45
Таблица дат занятий и номеров задач.
| Нед | 1В9 | 129 | 589-3 |
| 1 | 04.02 1-11 | 04.02 1-11 05.02 12 - 19 | 06.02 1-11 07.02 12 - 19 |
| 2 | 11.02 12 - 19 12.02 20 - 32 | 11.02 20 - 32 | 13.02 20 - 32 |
| 3 | 18.02 33 - 43 | 18.02 33 - 43 19.02 44 - 51 | 20.02 33 - 43 21.02 44 - 51 |
| 4 | 25.02 44 - 51 26.02 52 - 59 | 25.02 52 - 59 | 27.02 52 - 59 |
| 5 | 3.03 | 3.03 4.03 | 5.03 6.03 |
| 6 | 10.03 11.03 | 10.03 | 12.03 |
| 7 | 17.03 | 17.03 18.03 | 19.03 20.03 |
| 8 | 24.03 25.03 | 24.03 | 26.03 |
| 9 | 31.03 | 31.03 1.04 | 2.04 3.04 |
| 10 | 7.04 8.04 | 7.04 | 9.04 |
| 11 | |||
| 12 | |||
| 13 | |||
| 14 | |||
| 15 | |||
| 16 | |||
| 17 | |||
| 18 |
Определённый интеграл
Задача 1. Вычислить интеграл  .
.
При этом осуществляется повторение темы «интегрирование иррациональностей».
Решение. НОК(2,4) = 4, поэтому замена  . При такой замене
. При такой замене  ,
,  ,
, 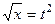 .
.  .
.
 =
=  =
=  =
=  =
=  =
=
 =
=  . Ответ.
. Ответ.  .
.
Задача 2. Вычислить интеграл 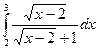 .
.
Решение. Сделаем замену  , тогда
, тогда  .
.
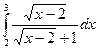 =
=  =
= 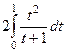 =
= 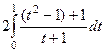 =
=
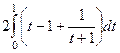 =
=  =
=  =
=  =
=  . Ответ.
. Ответ.  .
.
Задача 3. Вычислить интеграл  .
.
Решение. При замене  , если
, если  то
то  .
.
 =
=  =
=  =
=  =
=
 =
=  =
= 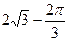 .
.
Ответ. 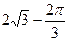 .
.
Рассмотрим 2 задачи на примерения интегрирования по частям в определённом интеграле.
Задача 4. Вычислить интеграл 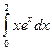 .
.
Решение. Применим метод интегрирования по частям,
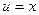
| 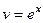
|

| 
|
Тогда
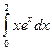 =
=  =
=  =
=  =
=  .
.
Ответ.  .
.
Задача 5. Вычислить интеграл  .
.
Решение. Тоже решается интегрированием по частям,
|
|
|
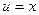 ,
,  , тогда
, тогда  ,
,  .
.
 =
=  =
=  =
=  =
= 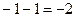 .
.
Ответ.  .
.
Замечание. Из строения графика видно, что ответ и должен был получиться отрицательным: изначально  имеет две одинаковые части площади над и под осью, и его интеграл был бы 0, а если мы умножаем на
имеет две одинаковые части площади над и под осью, и его интеграл был бы 0, а если мы умножаем на  , то сильнее увеличится по модулю именно та часть, которая дальше от 0, то есть расположенная ниже горизонтальной оси. Вот эти графики, зелёным показан
, то сильнее увеличится по модулю именно та часть, которая дальше от 0, то есть расположенная ниже горизонтальной оси. Вот эти графики, зелёным показан  , красным
, красным  .
.

Задача 6. Вычислить интеграл  .
.
Решение.  =
=  =
= 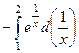
используя известное выражение  , получим:
, получим:
 =
=  =
=  .
.
Задача 7. Вычислить интеграл 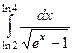
Решение. Сделаем замену  . Тогда
. Тогда  ,
,  ,
, 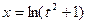 ,
,  , функция
, функция  монотонна, так что замена корректная. Теперь найдём новые границы: если
монотонна, так что замена корректная. Теперь найдём новые границы: если  , то
, то  . Тогда
. Тогда 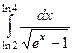 =
=  =
=  =
=  =
= 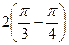 =
=  . Ответ.
. Ответ.  .
.
Задача 8. Вычислить интеграл  .
.
При этом осуществляется повторение темы «интегрирование тригонометрических функций».
Решение. Суммарная степень чётна, поэтому применяется замена
 , тогда
, тогда 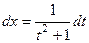 ,
, 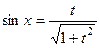 ,
,  .
.
Пересчитаем границы. 

 ,
, 

 .
.
Итак, подставим всё это в интеграл.
 =
=  =
=  =
=
=  =
=  =
=  =
=  =
=  . Ответ.
. Ответ.  .
.
Задача 9. Вычислить интеграл  .
.
При этом осуществляется повторение темы «элементарные преобразования, подведение под знак дифференциала».
Решение.  =
= 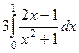 =
=  =
=
 =
=  =
=
 =
=  . Ответ.
. Ответ.  .
.
Задача 10. Вычислить интеграл  .
.
При этом осуществляется повторение темы «рациональные дроби».
Решение. Сначала представим дробь в виде суммы простейших.
 . При приведении к общему знаменателю, числитель получится такой:
. При приведении к общему знаменателю, числитель получится такой:
 , что равно
, что равно  ,
, 


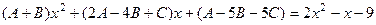

система:  решим её методом Гаусса.
решим её методом Гаусса.




 .
.
Здесь от 2-й строки отняли удвоенную 1-ю и от 3-й 1-ю, а затем от 3-й строки 2-ю. Основная матрица системы стала треугольной, и С находится сразу же:  . Тогда
. Тогда  и тогда
и тогда  . Из 1-го уравнения тогда уже получается
. Из 1-го уравнения тогда уже получается  .
.
Значит, исходный интеграл распадается на сумму 3 интегралов:  =
=  =
=
 =
=  =
=  .
.
Ответ.  .
.
Задача 10* на повторение, либо домашняя.
 =
= 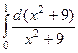 =
=  =
=  =
= 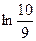 .
.
Приложения определённого интеграла.
Задача 11. Найти площадь фигуры, ограниченной линиями 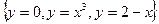 .
.
Решение. Построим чертёж:

Так как верхняя граница после точки 1 переходит с одной кривой на другую, то придётся разбить на сумму двух вычислений по каждой части отдельно:  +
+  . Итак, получим
. Итак, получим 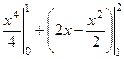 =
=  =
=  =
=  . Ответ.
. Ответ.  .
.
Вариант 11-Б. Найти площадь фигуры, ограниченной линиями  . Ответ.
. Ответ.  .
.
Задача 12. Найти площадь фигуры, ограниченной линиями:
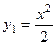 и
и  .
.
Решение. Рассмотрим чертёж, найдём точки пересечения графиков и увидим, какую часть плоскости они ограничивают.

График  имеет максимум в точке 0 и проходит выше, чем
имеет максимум в точке 0 и проходит выше, чем 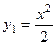 , у которой, напротив, там минимум. Точки перечечения
, у которой, напротив, там минимум. Точки перечечения  ,
,  . Все функции в интеграле чётные, фигура симметрична, можно вычислить площадь правой половины и удвоить:
. Все функции в интеграле чётные, фигура симметрична, можно вычислить площадь правой половины и удвоить:  =
=  =
=  =
= 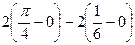 =
= 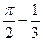 . Ответ.
. Ответ. 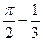 .
.
Задача 13. Найти площадь области, ограниченной линиями 
Решение.
 =
=  =
=  =
=  =
=  .
.
Чертёж:

Ответ.  .
.
Задача 14. Найти площадь фигуры, ограниченной линиями:  .
.
Решение. Чертёж:

 =
=  =
=  +
+ 
для раскрытия 1-го слагаемого, вспомним пример из лекйиц на интегрирование по частям, там делали именно этим методом.
Если  ,
,  ,
,  ,
,  то:
то:
 +
+  =
=  +
+  =
=

 +
+  =
=  =
=
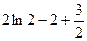 =
=  .
.
Ответ.  .
.
Задача 15. Найти объём, получающийся при вращении кривой  , при условии что
, при условии что  .
.
Решение.  =
=  =
=  =
= 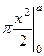 =
=  .
.
Ответ.  .
.
Замечание. Эта задача может быть интерпретирована физическим примером: сколько воды может поместиться в эллиптический параболоид. Ведь если график корня повернуть на 90 градусов, это парабола.
Задача 16. С помощью основной формулы объёмов тел вращения, доказать формулу объёма конуса  .
.
Решение. Для удобства применения основной формулы, повернём конус на 90 градусов, так, чтобы высота лежала на оси  .
.

На чертеже видно, что два катета имеют длины  и
и  . Тогда отрезок, вращением которого образована боковая поверхность конуса, находится на прямой
. Тогда отрезок, вращением которого образована боковая поверхность конуса, находится на прямой  .
.
|
|
|
 =
=  =
=  =
=  =
=  =
=  =
=  .
.
Ответ: формула доказана.
Задача 17. Найти длину 1 витка винтовой линии в пространстве 

Решение. В данном случае кривая параметрически задана, в 3-мерном пространстве. Формула  .
.
Производные:  .
.
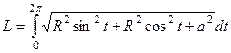 =
=  =
= 
Ответ. 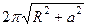 .
.
Замечание. Если была бы не винтовая линия, а окружность, а это было бы при параметре 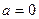 , то как раз бы и получалось
, то как раз бы и получалось  длина окружности.
длина окружности.
Задача 18. Найти длину кривой 
 .
.
Решение. Применяем формулу в плоскости  .
.
Производные:  .
.
 =
=  =
=  .
.
Но здесь важно учесть, что  во 2 четверти отрицателен, поэтому при сокращении корня и квадрата надо учесть знак модуля.
во 2 четверти отрицателен, поэтому при сокращении корня и квадрата надо учесть знак модуля.
 . Далее придётся разбить на 2 отрезка, чтобы устранить знак модуля на каждом по-своему:
. Далее придётся разбить на 2 отрезка, чтобы устранить знак модуля на каждом по-своему:
 =
=  =
=
 =
=  =
=
 =
=  = 15.
= 15.
Ответ. 15.
Замечание. Если бы не учли знак модуля и не разбили на 2 части, тогда получилось бы неверно, ведь эти части бы не складывались, а взаимно уничтожались.
Задача 19. Найти длину кривой, заданной в полярных координатах:  ,
,  .
.
Решение. Формула:  .
.
 ,
,  .
.
 =
= 
=  =
=  , дальше замена
, дальше замена  .
.
 ,
,  ,
,  ,
, 

 .
.
 =
=  =
=
 =
= 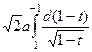 =
=  =
=  =
=
 . Ответ.
. Ответ.  .
.
 2020-04-07
2020-04-07 251
251







