Понятие случайной величины

Рассмотрим эксперимент с множеством исходов 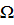. Случайной величиной  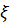называют функцию, которая каждому исходу  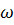из множества  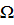ставит в соответствие некоторое действительное число.

Ограничимся рассмотрением случайных величин, множество значений которых конечно. Такие случайные величины называют дискретными.

Каждому значению x_i случайной величины 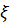 соответствует некоторое событие, наблюдаемое в эксперименте. Это событие будем обозначать 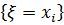, а его вероятность  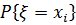или p_i. Перечень всех возможных значений случайной величины и соответствующих этим значениям вероятностей называют законом распределения случайной величины.  

Пример.  Эксперимент состоит вподбрасывании игральной кости и фиксации выпавшего на верхней грани числа. Задать на множестве исходов этого эксперимента какие-нибудь две случайные величины. Для каждой из них записать закон распределения.

Решение. Исходами данного эксперимента являются числа: 1, 2, 3, 4, 5, 6.

а) Определим случайную величину 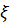 следующим образом: 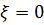, если выпало нечетное число очков, и 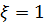, если выпало четное число очков.

В событие 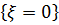 входят исходы: 1, 3, 5. Следовательно, вероятность 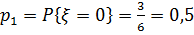. В событие  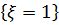входят исходы: 2, 4, 6. Следовательно, 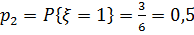. Зададим закон распределения в виде таблицы:

xi	0	1
pi	0,5	0,5

б) Определим случайную величину 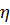 следующим образом: 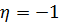, если выпала единица, 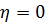, если выпало простое число, 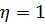, если выпало составное число.

Событие 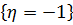 состоит из одного исхода 1; 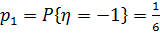. Событие  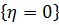состоит из исходов 2, 3, 5; 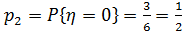. Событие  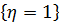состоит из исходов 4, 6; 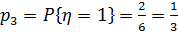. Зададим закон распределения в виде таблицы:

xi	-1	0	1
pi

 

3.2. Функция распределения
и числовые характеристики случайной величины

Пусть 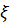 – случайная величина, наблюдаемая в эксперименте с множеством исходов 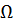. Возьмем любое конкретное действительное число х и рассмотрим исходы 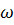, для которых выполняется неравенство 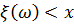. Эти исходы образуют некоторое подмножество множества 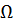, т.е. неравенством  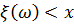определяется некоторое событие, наблюдаемое в данном эксперименте. Рассмотрим функцию, которая каждому действительному числу ставит в соответствие число, определяемое формулой 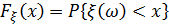. Эту функцию называют функцией распределения случайной величины .

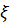Математическим ожиданием 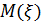 дискретной случайной величины 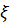, принимающей значения х₁, х₂, …, х_n с вероятностями p₁, p₂, …, p_n, называется число, вычисляемое по формуле:

.

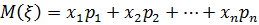Дисперсией 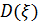 дискретной случайной величины 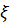, принимающей значения х₁, х₂, …, х_n с вероятностями p₁, p₂, …, p_n, называется число, вычисляемое по формуле:

.

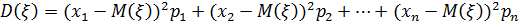Пример. Из ящика, содержащего 3 красных и 5 синих шаров, случайным образом и без возвращения отбираются 2 шара. Случайная величина 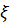 – число синих шаров в выборке.

а) Задать таблицей закон распределения .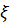

б) Найт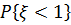и  и .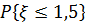

в) Найти функцию распределения случайной величины 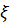 и построить ее график.

г) Вычислить математическое ожидание и дисперсию 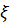[16].

Решение.

а) Случайными исходами описанного опыта являются неупорядоченные выборки без возвращения двух шаров из восьми, т.е. сочетания из 8 элементов по 2. Следовательно .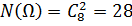

По условию случайная величина 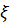 принимает три значения: 0, 1, 2. Исходами, благоприятствующими событию 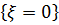, являются неупорядоченные выборки двух красных шаров из трех. Число таких выборок равно трем, следовательно 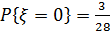. Исходами, благоприятствующими событию 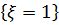, являются неупорядоченные выборки, в которые входят один синий и один красный шар. Число таких выборок равно  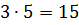(здесь 3 –т число способов выбрать красный шар из трех, 5 – число способов выбрать синий шар из пяти), следовательно 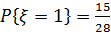. И, наконец, исходами, благоприятствующими событию 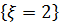, являются неупорядоченные выборки двух синих шаров из пяти. Число таких выборок 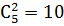, следовательно .

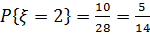Запишем закон распределения 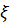 в виде таблицы:

xi	0	1	2
pi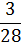

 

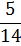
б) Событие 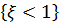 совпадает с событием 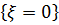. Значит вероятность .

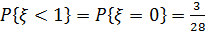Событие 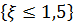 можно представить как сумму двух несовместных событи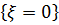й  и 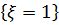, следовательно вероятность,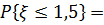
 .

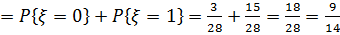в) Построим функцию распределения случайной величины :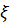

при 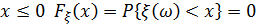, т.к. ни одного исхода, для которого 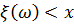, нет;

при ;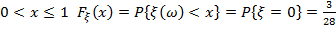

при ;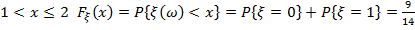

при .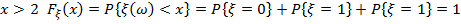

График функции распределения представлен на рис. 2.

 

 

 

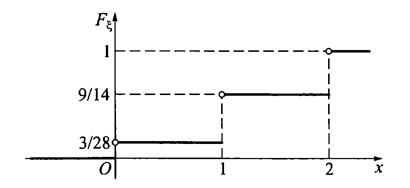
г) ;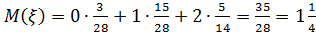

 

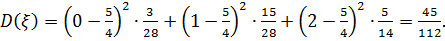
СПИСОК ЛИТЕРАТУРЫ

1. Бочаров П.П., Печенкин А.В. Теория вероятностей. Математическая статистика. – 2-е изд. – М.: ФИЗМАТЛИТ, 2005. – 296 с.

2. Виленкин Н.Я. Комбинаторика /Н.Я. Виленкин, А.Н. Виленкин, П.А. Виленкин. – М.: ФИМА, МЦНМО, 2006. – 400с.

3. Гмурман В.Е. Теория вероятностей и математическая статистика:
Учебное пособие. – 12-е изд., перераб. – М.: Высшее образование, 2006.
– 479 с.

4. Григорьев С.Г. Математика: учебник для студ.учреждений сред. проф. образования / С.Г. Григорьев, С.В. Иволгина; под ред. В.А. Гусева. –
12-е изд., стер. – М.: Издательский центр «Академия», 2016. – 416 с.

5. Золотаревская Д.И. Теория вероятностей: Задачи с решениями: Учебное пособие. – Изд. 2-е, перераб. и доп. – М.: Едиториал УРСС, 2003. – 168 с.

6. Морозова В.Л. Элементы комбинаторики: Учебное пособие / В.Л. Морозова, И.Н. Власова; Перм. гос. пед. ун-т. – Пермь, 2004. – 38 с.

7. Письменный Д.Т. Конспект лекций по теории вероятностей и математической статистике. – М.: Айрис-пресс, 2004. – 256 с.

8. Спирина М.С. Дискретная математика: Учебник для студ. учреждений сред. проф. образования / М.С. Спирина, П.А. Спирин. – М.: Издательский центр «Академия», 2004. – 368 с.

9. Тюрин Ю.Н. Теория вероятностей и статистика / Ю.Н. Тюрин, А.А. Макаров, И.Р. Высоцкий, И.В. Ященко – М.:МЦНМО: АО «Московские учебники», 2004. – 112 с.

10. Шабунин М.И. Математика. Алгебра. Начала математического анализа. Профильный уровень: методическое пособие для 11 класса / М.И. Шабунин, А.А. Прокофьев, Т.А. Олейник, Т.В. Соколова. – М.: БИНОМ. Лаборатория знаний, 2010. – 360 с.

11. http://combinatoric.ru.gg

12. http://mat.1september.ru/view_article.php?ID=201000409