Рациональной дробью называется дробь вида  , где
, где  и
и  - многочлены.
- многочлены.
Рациональная дробь называется правильной, если степень числителя  меньше степени знаменателя, в противном случае дробь называется неправильной.
меньше степени знаменателя, в противном случае дробь называется неправильной.
Простейшими называются правильные дроби вида:
1)  , где
, где  - целое число и
- целое число и  ;
;
2)  , где
, где  , т.е. квадратный трехчлен не имеет действительных корней,
, т.е. квадратный трехчлен не имеет действительных корней,  - целое число и
- целое число и  .
.
Интегралы от простейших дробей вычисляются по формулам:
1)  ;
;
2)  ;
;
3)  вычисляется с помощью подстановки
вычисляется с помощью подстановки  или по формуле:
или по формуле:  .
.
4)  заменой
заменой  приводится к виду:
приводится к виду: 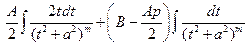 , где
, где  . (4)
. (4)
Первый из интегралов легко вычисляется:

 .
.
Второй из интегралов  вычисляется по рекуррентной формуле:
вычисляется по рекуррентной формуле:  . Эта формула сводит вычисление интеграла
. Эта формула сводит вычисление интеграла  к вычислению интеграла
к вычислению интеграла  с меньшим на единицу номером. При
с меньшим на единицу номером. При 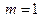 ,
,  . Например,
. Например,  .
.
Подставив найденные значения интегралов в формулу (4) и возвратившись к старой переменной по формуле  , вычислим интеграл.
, вычислим интеграл.
Интегрирование любой рациональной дроби сводится к разложению данной дроби на простейшие и интегрированию простейших дробей и многочленов. Порядок вычисления следующий:
1) если дана неправильная дробь, то выделить из нее целую часть, многочлен  , и остаток
, и остаток  , поделив числитель на знаменатель «уголком»;
, поделив числитель на знаменатель «уголком»;
2) разложить знаменатель дроби на линейные и квадратичные множители:
 , где
, где  - действительные корни уравнения
- действительные корни уравнения  ;
;  - квадратные трехчлены, не имеющие действительных корней;
- квадратные трехчлены, не имеющие действительных корней;
3) правильную рациональную дробь  разложить на простейшие:
разложить на простейшие: 


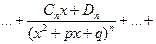

 ;
;
4)вычислить неопределенные коэффициенты 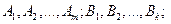

 , для чего привести последнее равенство к общему знаменателю, приравняв коэффициенты при одинаковых степенях
, для чего привести последнее равенство к общему знаменателю, приравняв коэффициенты при одинаковых степенях  в левой и правой частях и решить полученную систему линейных уравнений относительно искомых коэффициентов. Коэффициенты можно также найти, придавая
в левой и правой частях и решить полученную систему линейных уравнений относительно искомых коэффициентов. Коэффициенты можно также найти, придавая  различные числовые значения;
различные числовые значения;
5) проинтегрировать слагаемые многочлена 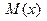 и полученные простейшие дроби.
и полученные простейшие дроби.
В результате интеграл от рациональной дроби  будет равен сумме интеграла от многочлена
будет равен сумме интеграла от многочлена 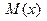 и интегралов от простейших дробей.
и интегралов от простейших дробей.
Пример 1. 30.
 , здесь
, здесь  , поскольку
, поскольку  , подынтегральное выражение представляет собой простейшую дробь. Интеграл вычисляется с помощью подстановки
, подынтегральное выражение представляет собой простейшую дробь. Интеграл вычисляется с помощью подстановки  :
: 



 .
.
Пример 1. 31.
 . Подынтегральное выражение представляет собой правильную дробь, поэтому выделять целую часть не нужно. Разложим знаменатель дроби на линейные и квадратичные множители:
. Подынтегральное выражение представляет собой правильную дробь, поэтому выделять целую часть не нужно. Разложим знаменатель дроби на линейные и квадратичные множители: 


 , затем разложим подынтегральное выражение на простейшие дроби:
, затем разложим подынтегральное выражение на простейшие дроби:
 , (5)
, (5)
Найдем коэффициенты  и
и  .
.
1 способ. Приведем правую часть равенства (5) к общему знаменателю и отбросим в полученном равенстве знаменатели. В результате будем иметь:  . (6)
. (6)
Подставим в (6)  , получим
, получим  (при
(при  второе и третье слагаемые правой части равенства (6) обращаются в нуль), отсюда
второе и третье слагаемые правой части равенства (6) обращаются в нуль), отсюда  .
.
Аналогично подставив в (6) последовательно  и
и  , получим:
, получим:  , отсюда
, отсюда  ;
;  , отсюда
, отсюда  .
.
2 способ. Составим систему уравнений для определения коэффициентов  и
и  . Равенство (4) выполняется тогда и только тогда, когда многочлены в левой и правой частях имеют равные коэффициенты при одинаковых степенях
. Равенство (4) выполняется тогда и только тогда, когда многочлены в левой и правой частях имеют равные коэффициенты при одинаковых степенях  :
:

 . Тогда
. Тогда

Решая систему трех линейных уравнений с тремя неизвестными, получим тот же результат:  ,
,  ,
,  .
.
Подставив найденные значения в (5) и проинтегрировав, окончательно получим: 
Пример 1. 32.
 . Разложим знаменатель на множители. Для этого решим биквадратное уравнение:
. Разложим знаменатель на множители. Для этого решим биквадратное уравнение:  . Отсюда
. Отсюда  или
или  . Итак, числитель и знаменатель раскладывается на линейные и квадратичные множители следующим способом:
. Итак, числитель и знаменатель раскладывается на линейные и квадратичные множители следующим способом:  .
.
Разложим подынтегральное выражение на простейшие дроби:
 , (7)
, (7)
приведем в равенстве (7) правую часть к общему знаменателю и отбросим его. Получим:  , (8)
, (8)
Найдем коэффициенты  и
и  , подставив последовательно
, подставив последовательно 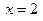 и
и  в (8), получим:
в (8), получим: 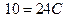 , откуда
, откуда  и
и  , откуда
, откуда  .
.
Поскольку в левой части равенства (8) нет коэффициента при  , а в правой части коэффициент при
, а в правой части коэффициент при  равен
равен  , поэтому получим:
, поэтому получим:  , откуда
, откуда  .
.
Подставим теперь  в (8):
в (8):  , учитывая найденные значения
, учитывая найденные значения  и
и  , получим
, получим  . Итак,
. Итак,


 .
.
При вычислении первого интеграла ( ) была использована формула замены переменной (см. пример 1.17.)
) была использована формула замены переменной (см. пример 1.17.)
Пример 1. 33.
 . Поскольку рациональная дробь неправильная, приходится делить многочлен
. Поскольку рациональная дробь неправильная, приходится делить многочлен  на многочлен
на многочлен  «уголком»:
«уголком»:

Получим частное  и остаток
и остаток  . Следовательно,
. Следовательно,
 . (9)
. (9)
Разложим знаменатель  на множители:
на множители:  . Множителю
. Множителю  соответствует сумма дробей
соответствует сумма дробей  , а
, а  соответствует
соответствует  . Итак,
. Итак,
 (10)
(10)
Приведем правую часть равенства (10) к общему знаменателю и отбросим его:
 . (11)
. (11)
Раскроем в правой части равенства (11) скобки и приравняем коэффициенты при одинаковых степенях  :
:
 ;
;

 ;
;
 ;
;
 ;
;
 .
.
Из этой системы последовательно находим:  ; подставив найденные значения в (10) и проинтегрировав каждое слагаемое, имеем:
; подставив найденные значения в (10) и проинтегрировав каждое слагаемое, имеем: 
 .
.
 2020-04-12
2020-04-12 167
167








