Интегрирование по частям

Пусть  и  - непрерывно дифференцируемые функции от , тогда имеет место формула:

                                       ,                                                               (3)

которая выражает правило интегрирования по частям.

С помощью формулы (3) вычисление интеграла  сводится к нахождению интеграла , который должен быть проще исходного либо ему подобным.

Порядок вычислений:

1) все подынтегральное выражение разбить на две части: одну обозначить через , другую – через ;

2) вычислить дифференциал  от функции по формуле  и функцию

, интегрируя ;

3) применить формулу интегрирования по частям;

4) вычислить интеграл  и записать окончательный ответ.

Основные типыинтегралов, берущихся по частям приведены в таблице 4.

Пример 1. 23.

. Это интеграл I типа. Поэтому положим . Отсюда , а  (при нахождении функции  произвольную постоянную  во внимание можно не принимать). Применяя формулу интегрирования по частям, получим:

.

Иногда формулу интегрирования по частям приходится применять два раза и более.

Пример 1. 24. Рассмотрим интеграл I типа.

.

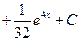Интегралы вида  или  сводятся к интегралам I типа с помощью формул тригонометрии: .

Таблица 4