Так как в потенциальном поле (выполнение условий (2.5)) криволинейный интеграл второго рода не зависит от формы пути интегрирования, то в качестве кривой L, вдоль которой будем вычислять криволинейный интеграл, возьмем ломаную линию, звенья которой параллельны осям координат. Зафиксируем начальную точку A( 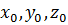 ) и соединим ее ломаной линией с текущей точкой B(x,y,z). Рассмотрим данный способ нахождения потенциала векторного поля на примере.
) и соединим ее ломаной линией с текущей точкой B(x,y,z). Рассмотрим данный способ нахождения потенциала векторного поля на примере.
Пример: вычислить потенциальную функцию векторного поля
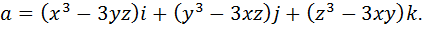
Начнем решение задачи с проверки условий (2.5) потенциальности заданного векторного поля.
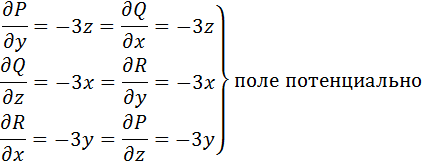
Тогда потенциальная функция
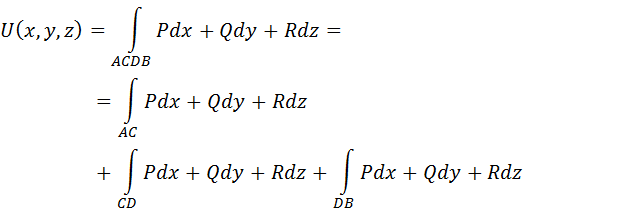
где
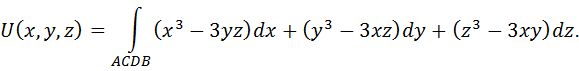
Рассмотрим интегралы вдоль каждого отрезка ломаной линии.
В данном примере в качестве начальной точки A( 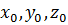 ) было взято начало координат A(0,0,0). Если же функции P(x,y,z), Q(x,y,z), и R(x,y,z) в начале координат не существуют, то обычно, в качестве начальной, берут точку с координатами A(1,1,1), либо любую другую.
) было взято начало координат A(0,0,0). Если же функции P(x,y,z), Q(x,y,z), и R(x,y,z) в начале координат не существуют, то обычно, в качестве начальной, берут точку с координатами A(1,1,1), либо любую другую.
Второй способ вычисления функции 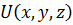 :
:
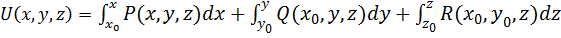 (2.6)
(2.6)
Для данной задачи найдем потенциальную функцию, используя формулу (2.6):

После окончательного решения задачи всегда следует делать проверку.
Пример: вычислить потенциальную функцию векторного поля двумя способами.

Проверим потенциальность векторного поля:
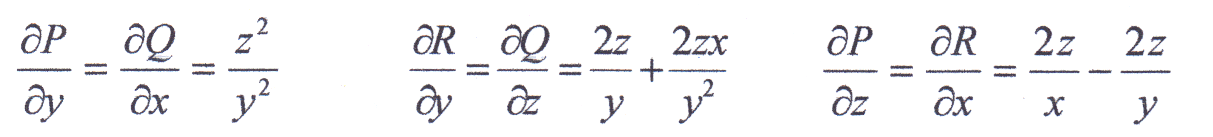
Условия (2.5) выполнены, следовательно, заданное поле потенциально.


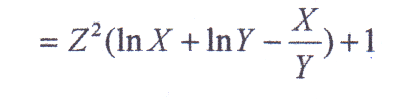
U(x,y,z) = Z²∙(ln x + ln y – (x/y)) + 1
2 способ вычисления потенциальной функции в соответствии с формулой (2.6):
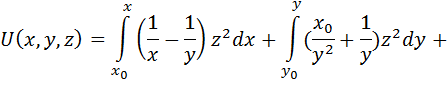
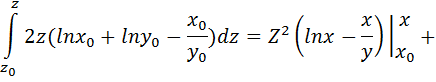
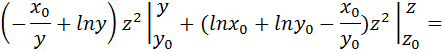
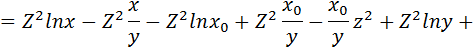
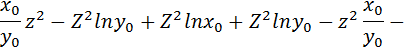
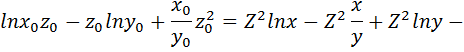
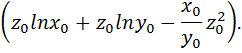
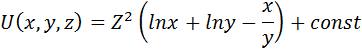
Проверим полученную потенциальную функцию:
Ответ: 
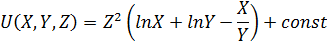
Пример: вычислить потенциальную функцию плоского векторного поля двумя способами.

Проверка условий потенциальности векторного поля.
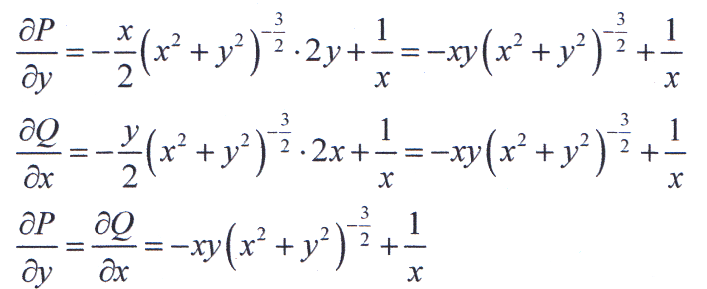
Следовательно, поле потенциально.
1-ый способ нахождения потенциальной функции.
Т.к. криволинейный интеграл 2-ого рода не зависит от формы пути интегрирования, примем за путь интегрирования ломаную линию АСВ, где линия АС параллельна оси ОХ, линия СВ параллельна оси ОУ. Т.к. функции P(x,y) и Q(x,y) не существуют в начале координат, то за начальную точку выберем точку с координатами (1,1).
2-ой способ (формула (2.6))
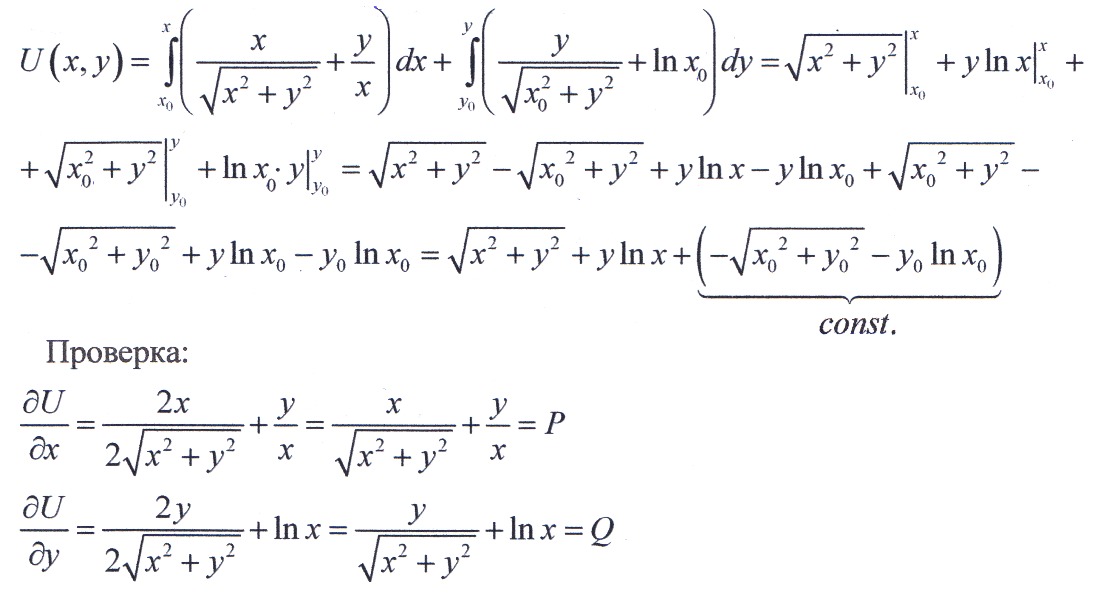
Оператор Гамильтона
Многие операции векторного анализа могут быть записаны в сокращенной и удобной для расчетов форме путем введения символического дифференцирующего вектора набла  , называемого оператором Гамильтона.
, называемого оператором Гамильтона.
Ротором вектора 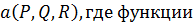
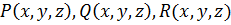 и их первые частные производные непрерывны в некоторой области 3-х мерного пространства, называется вектор, получаемый в результате векторного произведения символического вектора
и их первые частные производные непрерывны в некоторой области 3-х мерного пространства, называется вектор, получаемый в результате векторного произведения символического вектора 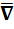 и вектора
и вектора 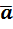 .
.
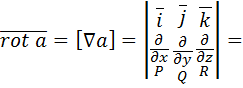
(2.7)

Если  , то векторное поле
, то векторное поле 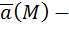 потенциально, т.к. если координаты вектора
потенциально, т.к. если координаты вектора 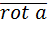 равны нулю, то мы получаем условия потенциальности векторного поля (2.5). Потому в задачах на нахождение потенциальной функции при проверке условий потенциальности векторного поля можно использовать либо условия потенциальности (2.5), либо вычислять
равны нулю, то мы получаем условия потенциальности векторного поля (2.5). Потому в задачах на нахождение потенциальной функции при проверке условий потенциальности векторного поля можно использовать либо условия потенциальности (2.5), либо вычислять 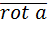 .
.
Пример: вычислить потенциальную функцию плоского векторного поля 
Решение начнем с нахождения 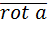 .
.
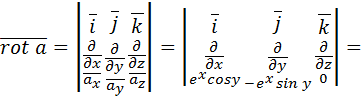
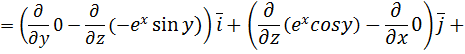
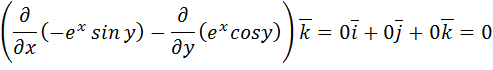
Следовательно, поле  является потенциальным. Найдем потенциальную функцию, используя формулу (2.6):
является потенциальным. Найдем потенциальную функцию, используя формулу (2.6):
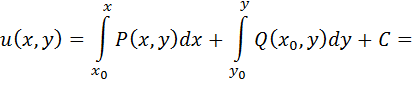
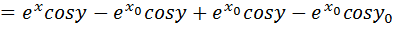
Проверка:
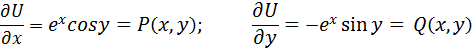
Кроме ротора векторного поля с помощью символического вектора набла можно найти градиент скалярной функции 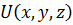 , путем простого умножения вектора набла на скалярную функцию
, путем простого умножения вектора набла на скалярную функцию 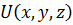
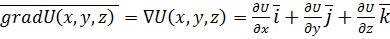 (2.8)
(2.8)
Скалярное произведение вектора 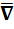 и вектора векторного поля
и вектора векторного поля 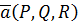 называется дивергенцией векторного поля. Дивергенция – величина скалярная и вычисляется следующим образом:
называется дивергенцией векторного поля. Дивергенция – величина скалярная и вычисляется следующим образом:
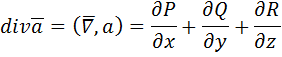 (2.9)
(2.9)
Формула Грина.
Для достаточно общего вида плоских областей D с положительно ориентированной границей Г справедлива формула Грина:
(2.10)
Формула Грина позволяет вычислить криволинейный интеграл второго рода по замкнутой линии Г, т.е. циркуляцию через двойной интеграл по области D, ограниченной этой кривой линией.
Пример: вычислить циркуляцию вектора
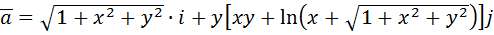
по окружности 
Циркуляция данного вектора равна:
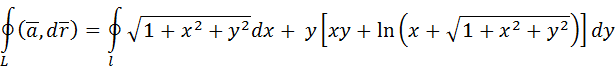
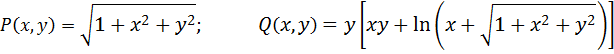
Находим частные производные:
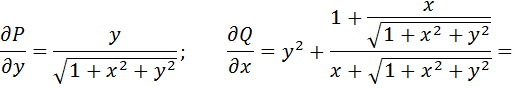
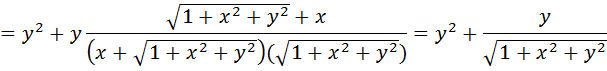
Тогда по формуле Грина (2.10):
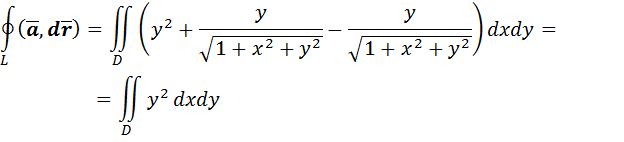
Т.к. кривая L является окружностью, то при вычислении двойного интеграла используем полярную систему координат: 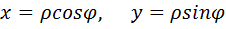
Тогда
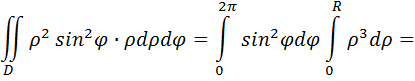

Пример: пользуясь формулой Грина, вычислить линейный интеграл в векторном поле 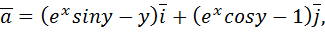 где L - верхняя часть полуокружности
где L - верхняя часть полуокружности  направление обхода контура от точки A(2;0) до точки О(0;0)
направление обхода контура от точки A(2;0) до точки О(0;0)
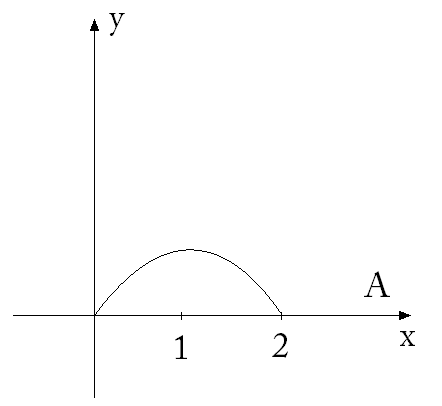
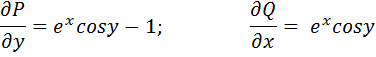
Уравнение окружности: 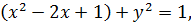
или 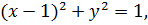 т.е. центр окружности рис. 2.4
т.е. центр окружности рис. 2.4
сдвинут по оси Ох вправо на одну единицу. Дополним дугу полуокружности отрезком прямой ОА. Кривая ОАО – становится замкнутой.
Тогда по формуле Грина (2.10):

По свойству двойного интеграла полученный интеграл равен площади области D, а радиус полуокружности R=1. Интеграл вдоль прямой ОА равен нулю (на ОА у=0; dy=0), следовательно, окончательный ответ - линейный интеграл равен 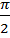 .
.
 2020-04-12
2020-04-12 4198
4198








