Пусть S – двухсторонняя ограниченная поверхность, заданная уравнением z = f(x,y), где f(x,y) – непрерывная функция в замкнутой области D – проекции поверхности S на плоскость XOY, а R(x,y,z) – непрерывная функция на поверхности S. Выберем верхнюю сторону поверхности S.
Разобьем поверхность S сетью кусочно-гладких линий на n частей ΔS1, ΔS2, …, ΔSn. Проекциями этих линий на плоскость XOY область D разобьется на n областей, обозначим их соответственно Δσ1, Δσ2, …, Δσn. Возьмем на каждой части ΔSi произвольную точку Mi(ξi,ηi,ζi) и составим интегральную сумму:
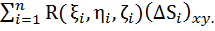
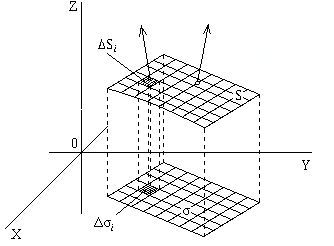
рис. 3.1
Так как сторона поверхности выбрана верхняя, то (ΔSi)xy = Δσi, а значит
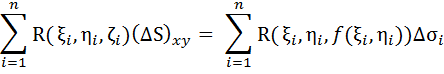
В правой части равенства имеем интегральную сумму для двойного интеграла от непрерывной функции R(x,y,f(x,y)) по области Dxy.
При стремлении к нулю шага разбиения поверхности S, Δσi также стремится к нулю. В пределе получаем формулу
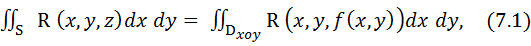 (3.1)
(3.1)
определяющую интеграл по верхней стороне поверхности S по переменным x и y через двойной интеграл по ее проекции на плоскость XOY.
Аналогичным образом устанавливается справедливость формул:
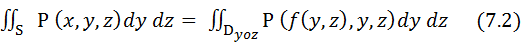 (3.2)
(3.2)
для функции P(x,y,z), непрерывной на двухсторонней поверхности S, заданной уравнением x = f (x,y) (Dyoz – проекция поверхности S на плоскость YOZ) и
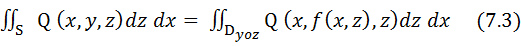 (3.3)
(3.3)
для функции Q(x,y,z), непрерывной на двухсторонней поверхности S, заданной уравнением y = f (x,z).
Если поверхность S такова, что для функций P(x,y,z), Q(x,y,z) и R(x,y,z), определенных в точках этой поверхности, интегралы (3.1), (3.2) и (3.3) существуют, то вводится понятие поверхностного интеграла «общего» вида по выбранной стороне поверхности:
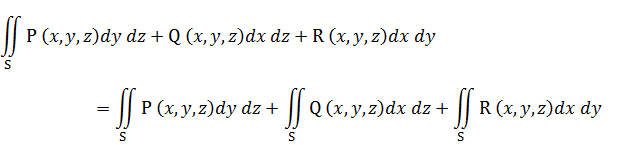
 2020-04-12
2020-04-12 206
206








