Пусть 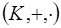 - коммутативное кольцо с единицей.
- коммутативное кольцо с единицей.
Определение. Элемент  называется делителем элемента
называется делителем элемента 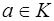 , а элемент
, а элемент 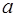 - кратным
- кратным  , если в
, если в  существует такой элемент
существует такой элемент  , что
, что  .
.
Запись 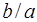 означает, что
означает, что  есть делитель
есть делитель 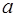 , запись
, запись  означает, что
означает, что 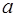 делится на
делится на 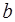 , или
, или 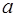 кратно
кратно  .
.
Примеры.
7.1. В кольце  многочленов с действительными коэффициентами многочлен
многочленов с действительными коэффициентами многочлен  делится на многочлен
делится на многочлен  , так как
, так как
 , где
, где  . В кольце
. В кольце  многочлен
многочлен  не делится на
не делится на 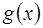 , так как
, так как  .
.
7.2. В кольце  целых гауссовых чисел
целых гауссовых чисел  . В самом деле:
. В самом деле:
 ,
,  .
.
7.3. В кольце 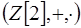 число
число  делится на число
делится на число  , так как
, так как
 ,
,
 .
.
7.4. В поле 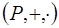 любой элемент
любой элемент 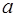 делится на любой отличный от нуля элемент
делится на любой отличный от нуля элемент  .
.
Действительно, если 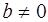 , то существует элемент
, то существует элемент  , такой, что
, такой, что  . Тогда имеем
. Тогда имеем  , причем
, причем  . Это означает, что
. Это означает, что  .
.
Обратимые элементы
Определение. Элемент  кольца
кольца 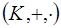 называется обратимым или делителем единицы, если в
называется обратимым или делителем единицы, если в 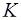 существует такой элемент
существует такой элемент  , что
, что 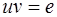 .
.
В этом случае пишут  .
.
Теорема. Пусть 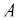 - множество всех обратимых элементов коммутативного кольца
- множество всех обратимых элементов коммутативного кольца  . Тогда умножение - алгебраическая операция в
. Тогда умножение - алгебраическая операция в  , алгебра
, алгебра 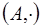 является абелевой группой.
является абелевой группой.
Примеры.
7.5. В кольце 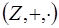 целых чисел обратимыми являются числа
целых чисел обратимыми являются числа  и
и 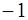 . Других обратимых элементов нет.
. Других обратимых элементов нет.
7.6. В кольце 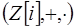 целых гауссовых чисел обратимыми являются числа
целых гауссовых чисел обратимыми являются числа  ,
,  ,
,  ,
, 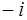 . Других обратимых элементов в этом кольце нет. Действительно, если элемент
. Других обратимых элементов в этом кольце нет. Действительно, если элемент  обратим, то найдется число
обратим, то найдется число  , такое, что
, такое, что  . Но тогда и
. Но тогда и  , т.е.
, т.е.
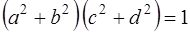 (1).
(1).
Так как 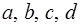 - целые числа и
- целые числа и  , то равенство (1) возможно лишь в случае
, то равенство (1) возможно лишь в случае  , т.е. в одном из четырех случаев:
, т.е. в одном из четырех случаев: 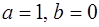 ;
;  ;
;  ;
; 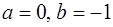 .
.
Это означает, что  может иметь лишь четыре значения:
может иметь лишь четыре значения:  ,
, 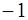 ,
,  ,
, 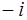 .
.
7.7. В кольце 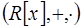 многочленов с действительными коэффициентами обратимыми являются многочлены нулевой степени, т.е. отличные от нуля действительные числа.
многочленов с действительными коэффициентами обратимыми являются многочлены нулевой степени, т.е. отличные от нуля действительные числа.
7.8. В кольце 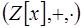 многочленов с целыми коэффициентами обратимыми являются числа
многочленов с целыми коэффициентами обратимыми являются числа  и
и  .
.
 2020-04-12
2020-04-12 686
686








