Определение. Элементы  и
и 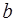 кольца
кольца  называются ассоциированными в
называются ассоциированными в  , если
, если  и
и  . (Обозначают
. (Обозначают  ).
).
Теорема. В области целостности  элементы
элементы  и
и 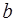 ассоциированы тогда и только тогда, когда существует такой обратимый в
ассоциированы тогда и только тогда, когда существует такой обратимый в  элемент
элемент  , что
, что  .
.
Примеры.
7.9. В кольце 
 ,
,  .
.
7.10. В кольце 
а)  ,
,  ,
,  ,
,  .
.
б) 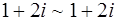 ,
,  ,
,  ,
,  .
.
7.11. В кольце 
 . Действительно:
. Действительно:

 , то есть
, то есть 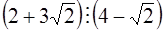 .
.
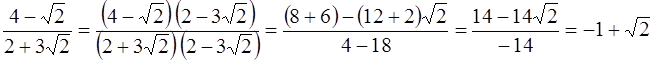
 , то есть
, то есть 
По определению,  .
.
Вычисления показывают, что  , причем элемент
, причем элемент  обратим в данном кольце.
обратим в данном кольце.
В самом деле:  .
.
7.12. В кольце  многочлен
многочлен  ,
,  ,
,  и т.п., вообще
и т.п., вообще  , где
, где 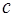 - любое действительное число, отличное от
- любое действительное число, отличное от  .
.
Любой, отличный от нулевого, многочлен  ассоциирован с многочленом
ассоциирован с многочленом  , где
, где  .
.
7.13. В кольце  многочлен
многочлен  ассоциирован с многочленами
ассоциирован с многочленами 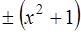 .
.
Любой, отличный от нулевого, многочлен  ассоциирован с многочленом
ассоциирован с многочленом  .
.
Простые и составные элементы области целостности
Пусть  - область целостности с единицей. Всякий элемент
- область целостности с единицей. Всякий элемент  кольца
кольца  делится на любой обратимый элемент кольца и на каждый ассоциированный с
делится на любой обратимый элемент кольца и на каждый ассоциированный с  элемент кольца. Такие делители называются тривиальными делителями элемента
элемент кольца. Такие делители называются тривиальными делителями элемента  .
.
Определение. Элемент области целостности  называется простым или неприводимым в
называется простым или неприводимым в  , если он отличен от нуля, необратим и имеет только тривиальные делители.
, если он отличен от нуля, необратим и имеет только тривиальные делители.
Определение. Элемент области целостности  называется составным или приводимым в кольце
называется составным или приводимым в кольце  , если он отличен от нуля и его можно представить в виде произведения двух необратимых элементов кольца.
, если он отличен от нуля и его можно представить в виде произведения двух необратимых элементов кольца.
Множество всех элементов области целостности распадается на четыре класса: 1) множество, содержащее один элемент - нуль; 2) множество всех обратимых элементов; 3) множество всех простых элементов; 4) множество всех составных элементов. Отметим, что в любом поле нет ни простых, ни составных элементов, т.е. последние два класса пустые.
Примеры
8.1. В кольце  указанные классы состоят из чисел:
указанные классы состоят из чисел:
1)  ; 2)
; 2)  ; 3)
; 3) 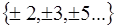 ; 4)
; 4)  .
.
8.2. В кольце  многочленов с комплексными коэффициентами классы состоят из многочленов: 1)
многочленов с комплексными коэффициентами классы состоят из многочленов: 1)  , 2)
, 2)  , 3) множество многочленов 1 степени, неприводимых над полем С, 4) множество многочленов степени
, 3) множество многочленов 1 степени, неприводимых над полем С, 4) множество многочленов степени  , приводимых над полем С.
, приводимых над полем С.
Определение. Говорят, что элемент  области целостности
области целостности  обладает однозначным разложением на простые множители, если для любых двух разложений элемента
обладает однозначным разложением на простые множители, если для любых двух разложений элемента  на простые множители
на простые множители  ,
,  имеем
имеем  и при соответствующей нумерации
и при соответствующей нумерации 
 .
.
Определение. Кольцо  называется факториальным, если оно есть область целостности и всякий отличительный от нуля необратимый элемент кольца обладает однозначным разложением на простые множители.
называется факториальным, если оно есть область целостности и всякий отличительный от нуля необратимый элемент кольца обладает однозначным разложением на простые множители.
Отметим, что любое поле есть факториальное кольцо, так как не имеет отличных от нуля необратимых элементов. Из теории чисел и теории многочленов известно, что кольцо  целых чисел, кольцо
целых чисел, кольцо  многочленов над числовым полем Р есть факториальные кольца.
многочленов над числовым полем Р есть факториальные кольца.
8.3. Какие из чисел  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  приводимы в кольце
приводимы в кольце  целых гауссовых чисел?
целых гауссовых чисел?
Решение:
В кольце  обратимы только числа
обратимы только числа  ,
,  .
.
а) Допустим, что число  является составным в данном кольце, значит
является составным в данном кольце, значит  представляется в виде произведения двух необратимых элементов данного кольца.
представляется в виде произведения двух необратимых элементов данного кольца.



 ,
,  ,
,  , иначе
, иначе  ,
,  - обратимые элементы, кроме того
- обратимые элементы, кроме того  ,
,  , поэтому
, поэтому  , значит
, значит 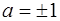 ,
,  . Отсюда
. Отсюда  , или
, или  . Тогда легко найти, что
. Тогда легко найти, что
 ,
,
полученные разложения числа  отличаются порядком следования сомножителей и обратимыми множителями.
отличаются порядком следования сомножителей и обратимыми множителями.
Число  составное в кольце
составное в кольце  , так как его можно представить в виде произведения двух необратимых элементов.
, так как его можно представить в виде произведения двух необратимых элементов.
б) Аналогично для числа  .
.
 ,
,  , причем
, причем  ,
,  . Поэтому равенство возможно лишь в случае
. Поэтому равенство возможно лишь в случае  ,
,  . Таких целых
. Таких целых 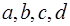 нет. Следовательно, число
нет. Следовательно, число  - простое в кольце
- простое в кольце  .
.
в) Для числа  имеем
имеем  , тогда аналогично пункту а)
, тогда аналогично пункту а)  ,
,  , причем
, причем  ,
, 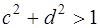 . Таких целых
. Таких целых  нет. Следовательно, число
нет. Следовательно, число  простое в кольце
простое в кольце  . То же легко получить для числа
. То же легко получить для числа  , оно также простое.
, оно также простое.
г) отметим, что числа  и
и  ;
;  и
и  ассоциированы.
ассоциированы.
 ,
, 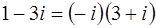 .
.
Для числа  аналогично пункту а) имеем
аналогично пункту а) имеем  ,
,  ,
,  , причем
, причем  ,
,  .
.
Поэтому: 1)  или 2)
или 2)  .
.
Отсюда 1)  ,
,  , тогда
, тогда  , или
, или  .
.
2)  ,
,  или
или  ,
,  , тогда
, тогда  или
или 
Отсюда для числа  получаем
получаем  . В остальных случаях разложения числа
. В остальных случаях разложения числа  простые множители будут отличаться порядком следования сомножителей и обратимыми множителями. Итак, доказали: число
простые множители будут отличаться порядком следования сомножителей и обратимыми множителями. Итак, доказали: число  составное в кольце
составное в кольце  . Для числа
. Для числа  ассоциированного с числом
ассоциированного с числом  получаем
получаем 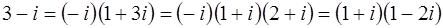 .
.
Легко доказать, что числа  ,
,  также составные, причем
также составные, причем
 ,
,  .
.
8.4. Покажите, что в кольце 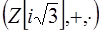 число
число  разлагается в произведение неприводимых множителей двумя различными способами.
разлагается в произведение неприводимых множителей двумя различными способами.
Решение.
В кольце  обратимы только числа
обратимы только числа  .
.
Пусть число 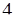 представляется в виде произведения двух необратимых в данном кольце элементов.
представляется в виде произведения двух необратимых в данном кольце элементов.
 ,
, 

 (1).
(1).
Учитывая, что  ,
,  - необратимые элементы, имеем
- необратимые элементы, имеем  ,
,  . Кроме того
. Кроме того  .
.
Тогда равенство (1) возможно в случаях:
1)  ,
, 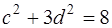 или
или  ,
,  . Таких целых
. Таких целых  нет.
нет.
2)  ,
,  ; это возможно при
; это возможно при  ,
, 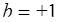 , тогда
, тогда
 , или при
, или при  ,
,  , тогда
, тогда  .
.
Отсюда получаем разложения числа  на необратимые множители:
на необратимые множители:
 (2)
(2)
 (3).
(3).
Отметим, что остальные разложения отличаются от указанных порядком следования сомножителей и обратимыми множителями.
Покажем, что разложения (2) и (3) существенно различны. Числа 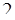 и
и  не ассоциированы. В самом деле
не ассоциированы. В самом деле
 , значит
, значит  не делится на
не делится на  и
и  в кольце
в кольце  . Далее покажем, что числа
. Далее покажем, что числа  и
и  - простые в кольце
- простые в кольце  .
.
Пусть число 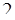 представляется в виде произведения двух необратимых в данном кольце элементов.
представляется в виде произведения двух необратимых в данном кольце элементов.
 ,
, 

 ,
,
учитывая, что
 ,
,  и
и  - целые,
- целые,
получаем
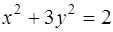 ,
, 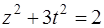 . Таких
. Таких  нет. Значит, число
нет. Значит, число 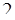 в кольце
в кольце  - простое.
- простое.
Для чисел  аналогично получаем
аналогично получаем

 ,
,  . Аналогично предыдущему видим, что таких целых
. Аналогично предыдущему видим, что таких целых  нет. Значит, числа
нет. Значит, числа  ,
,  простые в кольце
простые в кольце  .
.
Вывод: Число  в кольце
в кольце  имеет два существенно различных разложения на простые множители.
имеет два существенно различных разложения на простые множители.
8.5. Какие из элементов  ,
,  ,
,  ,
,  ,
,  ,
, 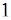 приводимы в кольце: а)
приводимы в кольце: а)  ; б)
; б)  ; в)
; в)  :
:
а) В кольце  множество обратимых элементов есть
множество обратимых элементов есть 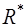 . В этом кольце имеем:
. В этом кольце имеем:
 ,
,  - обратимый элемент данного кольца,
- обратимый элемент данного кольца,
 ,
,
 ,
,
 ,
,
 ,
,  - обратимые элементы данного кольца.
- обратимые элементы данного кольца.
Видим, что в кольце  неприводим многочлен
неприводим многочлен  , приводимы многочлены
, приводимы многочлены  ,
,  ,
,  .
.
б) В кольце  множество обратимых элементов есть
множество обратимых элементов есть  .
.
Видим, что в кольце  неприводимы многочлены:
неприводимы многочлены:  ,
,  ,
,  ; приводимы многочлены:
; приводимы многочлены:  ;
;  ,
,  - обратимые элементы данного кольца;
- обратимые элементы данного кольца;
в) В кольце  множество обратимых элементов есть
множество обратимых элементов есть  .
.
В этом кольце
 ,
, 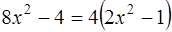 ,
,
 и
и  ,
,  - необратимые элементы данного кольца,
- необратимые элементы данного кольца,  ,
,  и
и  - необратимые элементы данного кольца.
- необратимые элементы данного кольца.
Видим, что в кольце  неприводимы многочлены:
неприводимы многочлены:  ; приводимы:
; приводимы:  ;
;  ;
;  ;
;  ;
;  - обратимый элемент данного кольца.
- обратимый элемент данного кольца.
 2020-04-12
2020-04-12 2391
2391