2020-04-12
117
Пусть функция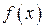 
определена и непрерывна при всех значениях 
из интервала 
.
Рассмотрим интеграл 
, где 
-любое число, лежащее правее 
, т.е. 
. Будем все время увеличивать и наблюдать, что происходит с интегралом.
Определение: Если существует конечный предел 
, то этот предел называется несобственным интегралом от функции 
на интервале 
.
Обозначение: 
.
Если этот предел существуетиконечен, то говорят, что несобственный интеграл сходится. Если предел не существует или равен бесконечности, то говорят, что несобственный интеграл расходится.
Аналогично вводится несобственный интеграл
для функции , непрерывной на интервале 
.
Если функции непрерывна на всей числовой оси, то можно рассмотреть интеграл
,
где 
- любое конечное число. Интеграл, стоящий слева, сходится тогда и только тогда, когда сходятся оба интеграла, стоящие справа.
Пример 1.
- не существует.
Следовательно, несобственный интеграл расходится.
Пример 2.
= 
= 
= 
=
= 
= 
.
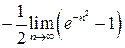Интеграл сходится.
Замечание. Для несобственных интегралов с бесконечными пределами интегрирования отсутствует понятие интегральной суммы, т.к. нельзя разбить бесконечный отрезок интегрирования на конечное число элементарных отрезков, имеющих конечную длину 
. В этом случае несобственный интеграл является не пределом интегральных сумм, а пределом определенного интеграла с переменным пределом интегрирования.
Оценка несобственных интегралов с бесконечными пределами интегрирования
Во многих практических случаях достаточно установить сходится или расходится данный интеграл и как-либо оценить его.
Теорема: Если для всех 
выполняется условие 
и интеграл 
сходится, то 
тоже сходится, причем 
.
Теорема: Если для всех выполняется условие 
и интеграл расходится, то тоже расходится.
Теорема: Если 
сходится, то сходится и интеграл , который в этом случае называется абсолютно сходящимся.
