Если функция 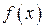 на отрезке
на отрезке 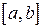 имеет конечное число точек разрыва 1-го рода, то отрезок разбивается на конечное число интервалов, где функция непрерывна и интеграл равен сумме интегралов, вычисленных на интервалах непрерывности функции.
имеет конечное число точек разрыва 1-го рода, то отрезок разбивается на конечное число интервалов, где функция непрерывна и интеграл равен сумме интегралов, вычисленных на интервалах непрерывности функции.
Пусть  определена и непрерывна при
определена и непрерывна при 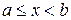 , а при
, а при  терпит разрыв 2-го рода, т.е.
терпит разрыв 2-го рода, т.е. 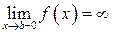 (см. рис. 3).
(см. рис. 3).

Рис.3.
В этом случае интегральную сумму построить можно, но она может принимать произвольно большие числовые значения в силу неограниченности  и, следовательно, не имеет предела. Поэтому построить определенный интеграл обычным способом нельзя.
и, следовательно, не имеет предела. Поэтому построить определенный интеграл обычным способом нельзя.
Рассмотрим интеграл  , где
, где  .
.
Определение. Если существует конечный предел  , то он называется несобственным интегралом от функции
, то он называется несобственным интегралом от функции  в пределах от
в пределах от  до
до  .
.
Обозначение:  .
.
Аналогично определяется несобственный интеграл для функции  , непрерывной на интервале
, непрерывной на интервале  :
:
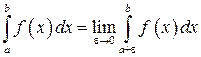 .
.
Если функция  имеет разрыв 2-го рода в некоторой точке
имеет разрыв 2-го рода в некоторой точке  , где
, где  , то несобственный интеграл запишется в виде
, то несобственный интеграл запишется в виде
 .
.
Исходный интеграл сходится, если сходятся оба интеграла, стоящие справа.
Теорема. Если первообразная 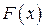 для функции
для функции  имеет конечный предел при
имеет конечный предел при  , т.е.
, т.е. 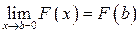 , то несобственный интеграл
, то несобственный интеграл 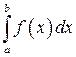 сходится и вычисляется по формуле Ньютона-Лейбница.
сходится и вычисляется по формуле Ньютона-Лейбница.
Доказательство. Рассмотрим интеграл
 , ч.т.д.
, ч.т.д.
Пример.
 =
= 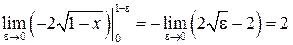 . Интеграл сходится.
. Интеграл сходится.
Оценка несобственных интегралов от разрывных функций
Теорема. Если на отрезке 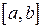 функции
функции  и
и  имеют разрыв 2-го рода только в точке
имеют разрыв 2-го рода только в точке  , причем во всех точках этого отрезка выполняются неравенства
, причем во всех точках этого отрезка выполняются неравенства  и интеграл
и интеграл  сходится, то сходится интеграл
сходится, то сходится интеграл  , и справедливо неравенство
, и справедливо неравенство
 .
.
Теорема. Если на отрезке 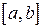 функции
функции  и
и  имеют разрыв 2-го рода только в точке
имеют разрыв 2-го рода только в точке  , причем во всех точках этого отрезка выполняются неравенства
, причем во всех точках этого отрезка выполняются неравенства 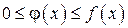 и интеграл
и интеграл  расходится, то расходится и интеграл
расходится, то расходится и интеграл  .
.
Теорема. Если знакопеременная на отрезке 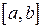 функция
функция  имеет разрыв 2-го рода только в точке
имеет разрыв 2-го рода только в точке  и несобственный интеграл
и несобственный интеграл  от абсолютной величины этой функции сходится, то сходится также интеграл
от абсолютной величины этой функции сходится, то сходится также интеграл 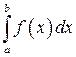 от самой функции. В этом случае он называется абсолютно сходящимся.
от самой функции. В этом случае он называется абсолютно сходящимся.
 2020-04-12
2020-04-12 1191
1191
