В математической статистике рассматриваются две основные задачи.
Первая задача состоит в том, чтобы указать способы сбора и группировки статистических сведений, полученных в результате наблюдений.
Вторая задача состоит в разработке методов анализа статистических данных в зависимости от целей исследования. К ним относятся:
оценка неизвестной вероятности события; оценка параметров распределения, вид которого неизвестен; оценка зависимости случайной величины от одной или нескольких случайных величин. Проверка статистических гипотез о виде неизвестного распределения или о величине параметров распределения, вид которого неизвестен.
В основе задач, решаемых методами математической статистики, лежит необходимость изучения совокупности однородных объектов, относительно некоторого качественного или количественного признака.
Совокупность всех объектов, подчиненных данному признаку, называется генеральной совокупностью. Число таких объектов называется объемом генеральной совокупности.
На практике обследование всех объектов генеральной совокупности не производится в силу излишней трудоёмкости или невозможности такого процесса. Обычно из всей совокупности отбирают ограниченное число объектов, которые и подвергают изучению. Такую случайно отобранную совокупность называют выборочной совокупностью или выборкой.
Элементы х1, х2, …, хn, попавшие в выборку называются вариантами, а их количество n – объемом выборки. Отобранные элементы располагают обычно в порядке их возрастания. Такая последовательность вариант называется вариационным рядом. Разность между максимальным и минимальным элементами называется размахом выборки.
Среди n элементов выборки могут встречаться повторяющиеся. Если, например, элемент х1 встречается n1 раз, х2 – n2 раз, …, хk – nk раз, то числа n1,n2, …,nk называются частотами вариант x1, x2, …, xk.
Расположенная в порядке возрастания вариант последовательность пар чисел, составленная из вариант и их частот (x1,n1), …, (xk,nk) называется статистическим распределением. При этом пользуются табличной записью:
| xi | x1 | x2 | … | xk |
| ni | n1 | n2 | … | nk |
Иногда вместо ni требуется использование относительных частот 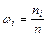 . Очевидно, что сумма частот всех элементов выборки равна:
. Очевидно, что сумма частот всех элементов выборки равна: 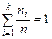 .
.
Пример 6.1. Написать вариационный ряд и статистическое распределение элементов выборки 5,0,7,4,0,10,3,4,4,7,8,10 – из числа дней в году, пропущенных по болезни учениками. Определить размах выборки.
Решение: Объем выборки n =12. Упорядочив элементы выборки по величине, получим вариационный ряд 0,0,3,4,4,4,5,7,7,8,10,10. Размах выборки z =10-0=10.
| xi | 0 | 3 | 4 | 5 | 7 | 8 | 10 |
| ni | 2 | 1 | 3 | 1 | 2 | 1 | 2 |
При большом объёме выборки её элементы объединяют в группы, представляя выборку в виде группированного статистического ряда. Для этого интервал, содержащий все элементы, разбивают на k непересекающихся интервалов. Вычисления упрощаются, если эти интервалы имеют одинаковую длину 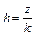 (здесь z – размах выборки, k – число интервалов). После того, как интервалы выбраны, определяются частоты – количество элементов ni* выборки, попавших в i -ый интервал, а сами элементы, попавшие в этот интервал, считаются равными его середине xi* (элемент, совпадающий с верхней границей интервала, относится к последующему интервалу).
(здесь z – размах выборки, k – число интервалов). После того, как интервалы выбраны, определяются частоты – количество элементов ni* выборки, попавших в i -ый интервал, а сами элементы, попавшие в этот интервал, считаются равными его середине xi* (элемент, совпадающий с верхней границей интервала, относится к последующему интервалу).
В зависимости от объёма выборки, число интервалов k группировки берется от 6 до 20. При этом следует помнить, что группировка вносит погрешности в дальнейшие вычисления. Эти погрешности растут с уменьшением числа интервалов. В процессе составления группированного статистического распределения подсчитываются также накопление частоты 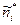 (накопленная частота i -го интервала равна сумме частот самого i ‑го и всех предыдущих интервалов). Относительные частоты ni* и накопленные частоты
(накопленная частота i -го интервала равна сумме частот самого i ‑го и всех предыдущих интервалов). Относительные частоты ni* и накопленные частоты 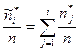 .
.
Пример 6.2. В результате опыта получены следующие результаты:
| 38 | 60 | 41 | 51 | 33 | 42 | 45 | 21 | 53 | 60 |
| 60 | 52 | 47 | 46 | 49 | 49 | 14 | 57 | 54 | 59 |
| 77 | 47 | 28 | 48 | 58 | 32 | 42 | 58 | 61 | 30 |
| 61 | 35 | 47 | 72 | 41 | 45 | 44 | 56 | 30 | 40 |
| 67 | 65 | 39 | 48 | 43 | 60 | 54 | 42 | 59 | 50 |
Найти размах выборки, число и длину интервалов, а также составить таблицу частот. Первый интервал 14-23.
Решение. Будем проводить группировку по интервалам равной длины h =23-14=9. Размах выборки z =77-14=63. Тогда необходимое число интервалов 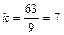 . Результаты группировки сведены в таблицу 6.1.
. Результаты группировки сведены в таблицу 6.1.
Таблица 6.1
| Номер интервала i | Границы интервала | Середина интервала хi* | Частота ni* | Относительная частота 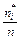 | Накопленная частота 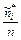 |
| 1 | 14-23 | 18,5 | 2 | 0,04 | 0,04 |
| 2 | 23-32 | 27,5 | 3 | 0,06 | 0,10 |
| 3 | 32-41 | 36,5 | 6 | 0,12 | 0,22 |
| 4 | 41-50 | 45,5 | 17 | 0,34 | 0,56 |
| 5 | 50-59 | 54,5 | 10 | 0,2 | 0,76 |
| 6 | 59-68 | 63,5 | 9 | 0,18 | 0,94 |
| 7 | 68-77 | 72,5 | 8 | 0,06 | 1,00 |
 2020-04-12
2020-04-12 2981
2981
