Зонная пластинка Френеля

Из дифракционной теории Френеля следует, что если закрыть все чётные или нечётные зоны, то волны, приходящие в т. Р, будут приходить с одинаковыми фазами и интенсивность света значительно увеличится. Пластинка, содержащая открытых зон обеспечивает освещённость в т. Р в раз большую, чем при открытой 1-ой зоне, т.е. такая пластинка ведёт себя как линза. На рисунке 7.6 показаны две пластинки Френеля с закрытыми чётными (слева) и нечётными (справа) зонами. Их называют амплитудными зонными пластинками Френеля.

Рис. 7.6 Амплитудные зонные пластинки Френеля с закрытыми чётными (слева) и нечётными (справа) зонами.

Эффективность зонной пластинки можно увеличить, если фазу чётных зон изменить на по отношению к фазе нечётных зон. Это легко осуществить, например, травлением стеклянной пластинки в области чётных или нечётных зон на глубину где – показатель преломления пластинки. Профиль такой пластинки, называемой бинарной фазовой пластинкой, представлен на рисунке 7.7.

Рис. 7.7 Профиль бинарной фазовой пластинки Френеля

Ещё больший эффект можно получить с помощью профильной фазовой пластинки (рис.7.8), в которой профиль каждой зоны изменяется таким образом, чтобы волны от каждой зоны приходили в т. Р с разностью фаз, равной нулю или кратной .

Рис 7.8 Профильная пластинка

7.3.2 Ближняя и дальняя зоны Френеля

Теория дифракции Френеля, несмотря на свой качественный характер, позволяет получить ряд полезных соотношений, характеризующих световое поле при дифракции на различных транспарантах. Выберем в качестве такого транспаранта круглое отверстие радиуса и рассмотрим дифракцию плоской световой волны на этом отверстии (рис. 7.9). В качестве точки анализа выберем точку P, находящуюся на оси отверстия и отстоящую от отверстия на расстояние z. На основании изложенной дифракционной теории Френеля

будем полагать, что на отверстии радиуса укладывается зон Френеля, тогда для последней -ой зоны имеем:

Рис. 7.9 Зоны Френеля на круглом отверстии

Отсюда, при условии , легко получить

Соответствующая стрелка прогиба сферической поверхности радиуса определяется из условия:

Из выражения (7.14) следует, что при фиксированном и увеличении расстояния 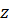за пределы отверстия будут выходить одна за другой периферийные зоны Френеля, пока, наконец, в пределах отверстия не останется одна первая зона . В этом случае, как следует из теории Френеля, интенсивность в т. P достигает максимума _,где –интенсивность света в самом отверстии. При дальнейшем увеличении в отверстии будет укладываться меньше одной зоны и интенсивность будет уменьшаться (рис. 7.10).

Рис. 7.10 Интенсивность света на оси отверстия

Значение , при котором отверстие совпадает с границей первой зоны Френеля, находится из (7.15) при

Оно называется дифракционной длиной светового пучка радиуса и обозначается _.Область расстояний z, удовлетворяющих неравенству

называется ближней зоной дифракции. В этой зоне световой пучок сохраняет структуру, задаваемую формой отверстия, а интенсивность света на оси примерно равна интенсивности исходной волны. Для точек ближней зоны в пределах отверстия помещается множество зон Френеля, волны от которых, интерферируя, обеспечивают постоянство поперечного сечения пучка. Зона, для которой

называется дальней зоной дифракции. В этой зоне интенсивность света на оси много меньше интенсивности исходной волны и уменьшается с ростом 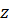. Следовательно, поперечное сечение пучка увеличивается, пучок расширяется. В дальней зоне на отверстии укладывается лишь часть первой зоны Френеля. Интерференция вторичных волн выражена слабее, пучок становится расходящимся.

Ввиду важности зависимости структуры светового пучка от числа зон Френеля последнее обозначают и называют числом Френеля. Значение определяется из (7.16) при :

Из (7.17 – 7.19) следует, что в ближней зоне , а в дальней зоне . Характер изменения поперечного размера светового пучка в ближней и дальней зонах иллюстрируется рисунком 7.11.