Теория дифракции Френеля

Рассмотрим распространение света с использованием принципа Гюйгенса-Френеля в случае ограниченной световой волны. Пусть P ₀ – точечный источник света с комплексной амплитудой A (рис.7.1). Требуется определить амплитуду U(P) колебаний в точке P.

Рис. 7.1 К объяснению теории дифракции Френеля

 

 

Если между точками P ₀ и P нет никаких препятствий и экранов, то решение очевидно[*]:

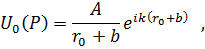
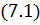
где 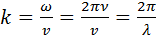 – волновое число;  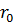– радиус сферического фронта волны в некоторый момент времени;  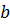– расстояние от точки C волнового фронта до точки P.

Будем полагать теперь, что волновой фронт волны, исходящей из точки P ₀ ограничен диафрагмой. Амплитуда колебаний в произвольной точке Q волнового фронта, очевидно, равна:

Некоторый элемент dσ волнового фронта в окрестности точки Q, являясь источником вторичной сферической волны (в соответствии с принципом Гюйгенса), создаёт в точке P элементарное возмущение, амплитуда которого:

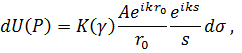
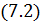
где s – расстояние QP; K(γ) – коэффициент наклона, введённый Френелем и учитывающий зависимость вклада элемента dσ в поле в точке P от угла γ между нормалью к dσ и направлением на точку P. По мнению Френеля, этот коэффициент должен иметь монотонно убывающий характер и обращаться в ноль при γ = 90º (рис.7. 2). Другими словами, коэффициент K(γ) имеет в точке C (γ = 0) максимальное значение и монотонно убывает до нуля в некоторой точке D волнового фронта (рис.7. 1).

 

Рис. 7.2 Примерный вид углового коэффициента

 

При наличии диафрагмы между P ₀ и P возмущение в точке P будет определяться той частью σ волнового фронта, которая не загораживается препятствием. Поэтому полное возмущение:

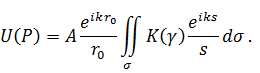
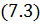
Для того, чтобы вычислить интеграл (7.3), воспользуемся так называемыми зонами Френеля. Построим вокруг точки P сферы с радиусами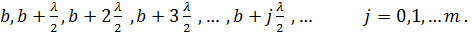   

Сферы делят волновой фронт σ на ряд зон 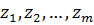 – зоны Френеля. Поскольку  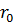и b велики по сравнению с λ, то можно считать, что в пределах отдельной j -ой зоны K(γ) = K_j = const и тогда:

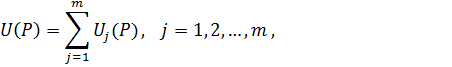
где

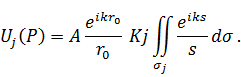
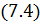
В интеграле (7.4) перейдем к новым переменным. Для этого учтём, что телесный угол dω, опирающийся на dσ равен:

 

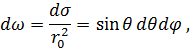
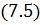
где θ и φ – полярный и аксиальный углы телесного угла. Кроме того, по теореме косинусов, имеем:

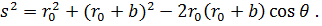
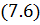
После дифференцирования (7.6) получаем:

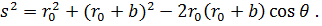
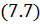
Выражения (7.5) и (7.7) позволяют выразить площадь элемента dσ в виде:

следовательно, интеграл (7.4) для j -ой зоны имеет вид:

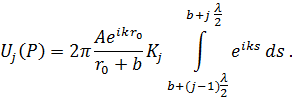
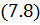
Входящий в (7.8) интеграл вычислим отдельно:

.

 

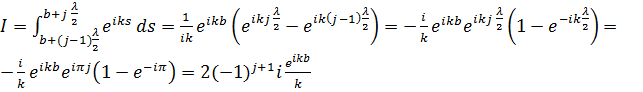Таким образом, вклад j -ой зоны в поле в точке P определяется выражением:

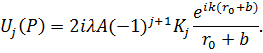
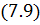
Заметим, что вклады следующих друг за другом зон имеют разные знаки. Результирующая амплитуда колебаний в точке P получится в виде:

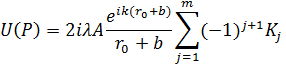
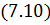
Знакочередующуюся сумму угловых коэффициентов с учётом монотонного характера изменения функции K(γ) вычислим по методу Шустера:

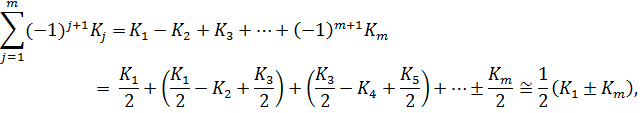
где знак перед 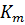 «+» при m – нечётном и «-» при m – чётном. Отметим, что в последнем выражении все члены в скобках были приняты равными нулю вследствие указанной монотонности изменения коэффициентов .

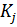Окончательно для поля в точке P получаем:

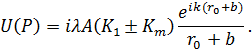
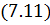
Полученное выражение с учётом (7.9) позволяет трактовать суммарное поле от всех зон волнового фронта в виде полусуммы полей от 1-ой и последней зон, т. е.:

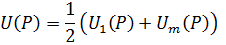
Этот результат вызывает на первый взгляд совершенно очевидный и недоуменный вопрос: «Почему на поле в точке P не сказывается вклад всех остальных зон Френеля?». Математически ответ на него дает изложенный метод вычисления сумм угловых коэффициентов, однако кроме предположения о монотонности их изменения за этим методом ничего не стоит. Френель объяснил полученный результат следующим образом. Волны от соседних зон приходят в точку P в противофазе и, интерферируя, «гасят» друг друга. Поэтому окончательный вклад обеспечивают нескомпенсированные колебания первой и последней зон. Такое объяснение позволило Френелю уточнить принцип Гюйгенса в том, что результирующее поле вторичных источников образуется в результате когерентного сложения их колебаний (интерференции). В настоящее время принцип Гюйгенса используется всегда с учётом указанного уточнения и называется принципом Гюйгенса-Френеля.

Формула (7.11) даёт правильный результат и при отсутствии между P ₀ и P диафрагм, ограничивающих волновой фронт. Действительно, в этом случае можно считать 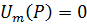, т.к.  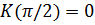и тогда   

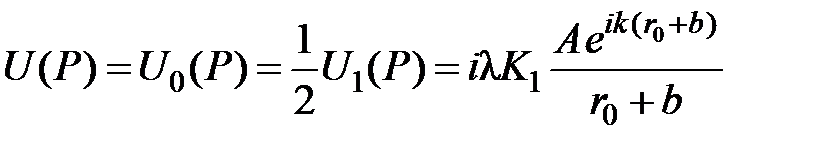                                          (7.12)

Если в (7.12) наложить условие 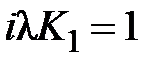, то, во-первых, выражение (7.12) полностью совпадёт с известным выражением (7.1) для сферической волны, а, во-вторых, можно найти максимальное значение углового коэффициента.

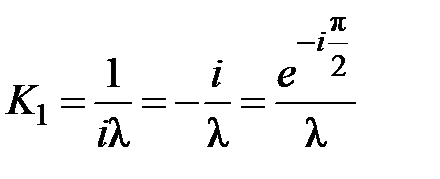             ,                                                                (7.13)

Множитель 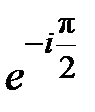 в (7.13) можно объяснить, если предположить, что вторичные волны отстают по фазе на  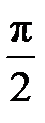от первичной волны. Наличие другого множителя  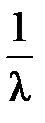является следствием введения при выводе элемента  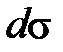волнового фронта и выяснением его физического смысла, как и физического смысла углового коэффициента, мы заниматься не будем.[†]

Рассмотрим частные случаи:

1. Открыта половина 1-ой зоны Френеля.

Из (7.9) при 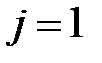 получаем:

                                                 

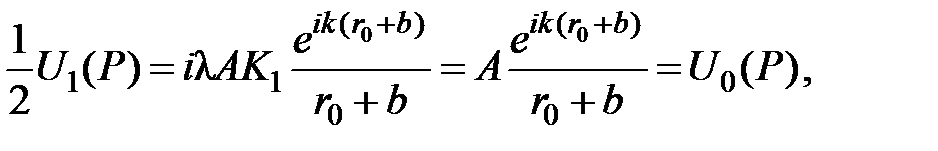
это означает, что поле в точке P в отсутствии диафрагм равно половине поля, которое производит 1-ая зона Френеля.

2. Открыта первая зона Френеля.

В этом случае

                                                                

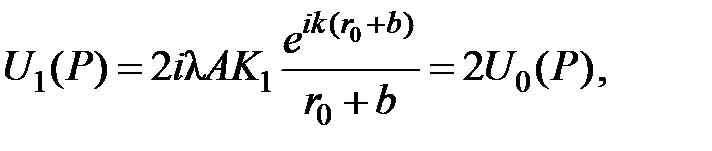
 т.е. поле в 2 раза больше и, следовательно, интенсивность в 4 раза больше, чем в отсутствии диафрагм.

3. Все зоны открыты, кроме первой.

В этом случае из (7.10) получаем

                           

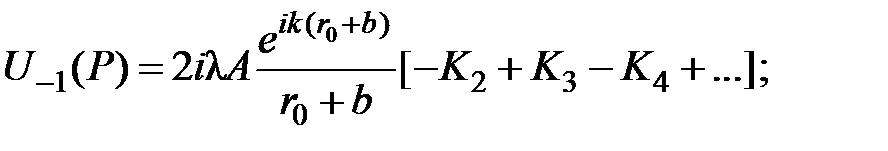
Используя метод Шустера для суммы в скобках, получаем значение 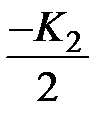, а поскольку  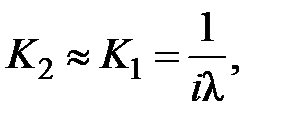имеем

                              .

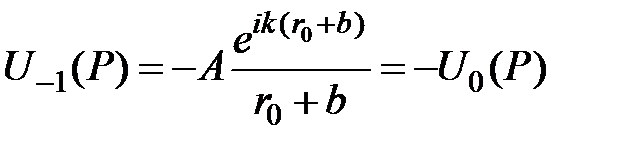Полученный результат означает, что в центре геометрической тени от непрозрачного диска, закрывающего первую зону Френеля должно наблюдаться светлое пятно с интенсивностью равной интенсивности в т. P при отсутствии диска. Исторически этот неочевидный с точки зрения геометрической и корпускулярной теории света вывод послужил серьёзным доказательством в пользу теории дифракции Френеля. В 1818 году Френель представил свою теорию на соискание премии Французской Академии Наук. Член комитета по премиям Пуассон, засомневавшись в наличии светлого пятна, провёл соответствующий опыт, который вначале не подтвердил предсказание Френеля. Лишь впоследствии другой член комитета – Араго, экспериментально доказал, что действительно при дифракции света от круглого непрозрачного экрана в центре тени возникает светлое пятно, предсказанное теорией. Тогда же была выяснена причина отрицательного результата опыта Пуассона. Она заключалась в неточном совпадении краёв непрозрачного диска с границей первой зоны Френеля. Это пятно вошло в историю оптики, как пятно Пуассона.