Интегральная теорема Гельмгольца-Кирхгофа

Кирхгоф придал идее Гюйгенса-Френеля строгий математический вид, что позволило ему не только получить аналитическое выражение для углового коэффициента, но и создать теорию, позволяющую находить количественные решения различных дифракционных задач.

Рассмотрим монохроматическую скалярную волну в вакууме

где амплитуда колебаний, зависящая от координат  Эта волна удовлетворяет волновому уравнению:

 где 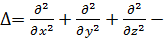оператор Лапласа. После подстановки (7.22) в (7.23) получаем дифференциальное уравнение Гельмгольца для определения функции

где волновое число.

Пусть 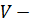 объём, ограниченный некоторой замкнутой поверхностью , а  некоторая точка внутри этого объёма (рис. 7.14). Будем считать эту точку началом системы координат .

Рис 7.14 К выводу интегральной теоремы Гельмгольца-Кирхгофа

Предположим также, что  имеет непрерывные производные первого и второго порядка внутри объёма и на его поверхности . Пусть функция  любая другая функция, удовлетворяющая тем же условиям, что и функция . Тогда для функций  и  справедлива вторая теорема Грина:

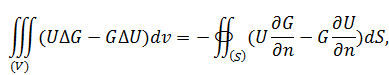
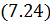
где  означает дифференцирование функции по внутренней поверхности нормали к поверхности .

Если в качестве  выбирать функцию, которая также удовлетворяла бы уравнению Гельмгольца, то есть

 то левая часть выражения (7.24) будет равна нулю, поскольку

Выберем функцию  (функцию Грина) в виде:

Эта функция удовлетворяет условию (7.25) и поскольку она имеет особенность в точке , исключим эту точку из рассматриваемого объёма, окружив её сферой 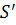 малого радиуса .

Теперь уравнение (7.24) принимает вид:

Учтём, что

тогда второе слагаемое в левой части (7.26) с учётом (7.27) при стремлении  к нулю преобразуется следующим образом:

И теперь (7.26) принимает вид

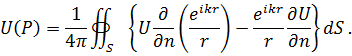
Соотношение (7.28), известное как интегральная теорема Гельмгольца- Кирхгофа, показывает, что для определения поля в некоторой точке  необходимо знать значение поля  и его производной  на замкнутой поверхности . Из него следует, что законы, управляющие вкладами от различных элементов поверхности, сложнее, чем предполагал Френель. Тем не менее Кирхгоф показал, что в большинстве случаев на практике его можно привести к простой формулировке, эквивалентной принципу Гюйгенса-Френеля и, кроме того, определить точное выражение для углового коэффициента, который в теории Френеля остался неопределенным.