Рассмотрим монохроматическую волну, идущую от источника света  сквозь отверстие в непрозрачном экране. Пусть
сквозь отверстие в непрозрачном экране. Пусть  – точка, в которой необходимо определить амплитуду световых колебаний
– точка, в которой необходимо определить амплитуду световых колебаний  Далее, пусть размеры отверстия велики по сравнению с длиной волны
Далее, пусть размеры отверстия велики по сравнению с длиной волны  (рис. 7.15).
(рис. 7.15).
Рис. 7.15 К выводу дифракционного интеграла Кирхгофа
Согласно интегральной теореме Кирхгофа, окружим точку  замкнутой поверхностью
замкнутой поверхностью  , образованной тремя участками: плоскостью отверстия
, образованной тремя участками: плоскостью отверстия  , непрозрачной частью экрана
, непрозрачной частью экрана  , сферой достаточно большого радиуса
, сферой достаточно большого радиуса  Тогда для поля в точке
Тогда для поля в точке  из (7.28) имеем
из (7.28) имеем
 |  |
Для вычисления интеграла (7.29) Кирхгоф сформулировал граничные условия, заключающиеся в том, что значения  и
и  отличны от нуля лишь в пределах отверстия и, кроме того, эти значения не отличаются от тех, которые имели бы на
отличны от нуля лишь в пределах отверстия и, кроме того, эти значения не отличаются от тех, которые имели бы на  в случае отсутствия экрана, то есть:
в случае отсутствия экрана, то есть:
на  :
: 

на  :
:  где
где  поле на
поле на  от источника в точке
от источника в точке 

а  производная от поля
производная от поля  по нормали
по нормали  к
к  , которая согласно (7.7) равна
, которая согласно (7.7) равна 
Значениями  и
и  на поверхности
на поверхности  можно пренебречь из простых соображений, например; если поле в
можно пренебречь из простых соображений, например; если поле в  возникает в момент времени
возникает в момент времени  , то в момент времени
, то в момент времени  его дальняя граница имеет радиус
его дальняя граница имеет радиус 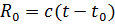 , следовательно, при
, следовательно, при  поле и его производная на
поле и его производная на 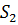 равны нулю.
равны нулю.
Таким образом, из (7.29) получаем:
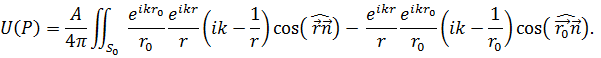
Полученное выражение известно в литературе как дифракционный интеграл Кирхгофа. При решении оптических задач обычно выполняются условия:
 и
и  , поэтому имеем k
, поэтому имеем k  и k
и k  , следовательно, пренебрегая в нем членами
, следовательно, пренебрегая в нем членами  и
и  , получаем:
, получаем:
 |  |
где  угол между векторами
угол между векторами  ,
,  дополнительный до
дополнительный до  угол между векторами
угол между векторами  (рис. 7.15).
(рис. 7.15).
Выражение (7.30) называют дифракционным интегралом Френеля  Кирхгофа в оптическом приближении. Если в качестве поверхности
Кирхгофа в оптическом приближении. Если в качестве поверхности  выбрать не плоскость диафрагмы, а сферу с центром в точке
выбрать не плоскость диафрагмы, а сферу с центром в точке  (рис.7.16), то тогда
(рис.7.16), то тогда  и интеграл (7.30) принимает вид:
и интеграл (7.30) принимает вид:
Рис. 7.16 Опорная поверхность – сфера с центром в т. 

Это выражение соответствует принципу Гюйгенса  Френеля, поскольку
Френеля, поскольку  является фронтом волны, а элементарный вклад элемента
является фронтом волны, а элементарный вклад элемента  в поле точки
в поле точки  равен
равен
 |  |
где

имеет смысл коэффициента наклона.
Отметим, что (7.31) полностью совпадает с формулой (7.2) в теории Френеля. Значительное отличие заключается в том, что Кирхгоф определил аналитическое выражение для этого коэффициента. При 
 принимает максимальное значение
принимает максимальное значение  , которое полностью совпадает с выражением, полученным Френелем. Однако, в отличие от Френеля, полагавшем, что при
, которое полностью совпадает с выражением, полученным Френелем. Однако, в отличие от Френеля, полагавшем, что при  коэффициент наклона должен обращаться в нуль, Кирхгоф доказал, что
коэффициент наклона должен обращаться в нуль, Кирхгоф доказал, что

то есть

Обратим внимание на то, что, исходя из формулы (7.30), можно сделать следующий вывод. Если точки  поменять местами, то интеграл (7.30) сохранит свой вид. Это означает, что точечный источник, находящийся в точке
поменять местами, то интеграл (7.30) сохранит свой вид. Это означает, что точечный источник, находящийся в точке  , производит в точке
, производит в точке  такое же действие, которое производит точечный источник равной интенсивности в
такое же действие, которое производит точечный источник равной интенсивности в  , находясь при этом в точке
, находясь при этом в точке  . Сформулированное положение называется теоремой взаимности Гельмгольца.
. Сформулированное положение называется теоремой взаимности Гельмгольца.
Если в плоскости диафрагмы ввести систему координат  то обобщая (7.30) можно записать:
то обобщая (7.30) можно записать:
 |  |
где  поле в плоскости отверстия диафрагмы (в рассматриваемом случае
поле в плоскости отверстия диафрагмы (в рассматриваемом случае 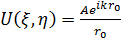 ). Выражение (7.32) можно записать в виде, отражающем принцип Гюйгенса
). Выражение (7.32) можно записать в виде, отражающем принцип Гюйгенса  Френеля
Френеля

где комплексная амплитуда колебаний вторичных источников на  ;
;
 (7.33)
(7.33)
Из (7.33) следует, что амплитуда вторичной волны отличается от амплитуды первичной множителем  , колебания вторичных волн отстают от колебаний первичной волны на
, колебания вторичных волн отстают от колебаний первичной волны на  (множитель – i), а зависимость амплитуды вторичных волн от направления определяется выражением
(множитель – i), а зависимость амплитуды вторичных волн от направления определяется выражением  .
.
Принцип Бабине. При практическом изучении дифракционных задач очень часто возникает необходимость в рассмотрении дифракционных полей от объектов, взаимно дополняющих друг друга. Дополнительными здесь называются такие объекты, когда отверстие в одном экране совпадает с другим экраном, так, например, круглому отверстию в плоскости одного экрана соответствует плоский диск, который дополняет экран до сплошной поверхности (рис. 7.17).
Рис. 7.17 Иллюстрация принципа Бабине
В этом случае принцип Бабине утверждает, что результаты, полученные для расчета задачи дифракции на плоском диске можно сразу перенести на случай дифракции на плоском дополнительном экране.
Пусть  и
и  – комплексные амплитуды дифракционного поля от двух дополнительных объектов, когда их помещают между источником и плоскостью наблюдения. Тогда, поскольку эти поля получены одно -
– комплексные амплитуды дифракционного поля от двух дополнительных объектов, когда их помещают между источником и плоскостью наблюдения. Тогда, поскольку эти поля получены одно -  при интегрировании по отверстию, а другое -
при интегрировании по отверстию, а другое -  по остальной поверхности, то в сумме они дают поле, которое получится при отсутствии экранов, т.е.
по остальной поверхности, то в сумме они дают поле, которое получится при отсутствии экранов, т.е.  С другой стороны, если
С другой стороны, если  то
то  , т. е. в точках, где
, т. е. в точках, где  равно нулю фазы
равно нулю фазы  и
и  различаются на π, а интенсивности
различаются на π, а интенсивности 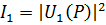 и
и  одинаковы.
одинаковы.
7.4.3 Дифракционные интегралы Френеля и Фраунгофера
Для дальнейшего введём системы координат  и
и  , в которых находятся
, в которых находятся  и
и  соответственно (рис. 7.18). Будем считать, что оси
соответственно (рис. 7.18). Будем считать, что оси  и
и  взаимно параллельны. Ось
взаимно параллельны. Ось 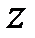 параллельна нормали
параллельна нормали  к плоскости диафрагмы и является общей для всех трёх систем.
к плоскости диафрагмы и является общей для всех трёх систем.
Рис 7.18 К выводу дифракционных интегралов Френеля и Фраунгофера
При вычислении интеграла (7.32) обычно используют следующие приближения:
1. Величина  изменяется незначительно около величины
изменяется незначительно около величины  , где
, где  -угол между прямой
-угол между прямой 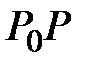 и осью
и осью 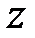 .
.
2. Модуль вектора  также незначительно изменяется около значения
также незначительно изменяется около значения  и изменения
и изменения 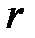 в знаменателе (7.32) не оказывает заметного влияния на точность определения поля в точке
в знаменателе (7.32) не оказывает заметного влияния на точность определения поля в точке  .
.
При сделанных допущениях получаем
 (7.34)
(7.34)
Выразим  в экспоненте (7.34), используя следующие очевидные соотношения:
в экспоненте (7.34), используя следующие очевидные соотношения:
 . (7.35)
. (7.35)
Из (7.35), исключив  , находим
, находим

При условиях  и
и  из (7.35), используя разложение в ряд Тейлора, получаем:
из (7.35), используя разложение в ряд Тейлора, получаем:
 , (7.36)
, (7.36)
при этом погрешность вычисления  не превышает первого отброшенного в разложении члена
не превышает первого отброшенного в разложении члена
 . (7.37)
. (7.37)
Соотношение (7.34) с учётом (7.36) принимает вид:
 (7.38)
(7.38)
Интеграл (7.38) называется дифракционным интегралом Френеля. Поскольку при выводе интеграла было использовано разложение в ряд, следует оценить границы его применимости. При вычислении интегралов от осциллирующих функций погрешность считается допустимой, если величина отбрасываемой фазы не превышает  , то есть
, то есть  . С учётом (7.37) для точки x=y=0 имеем:
. С учётом (7.37) для точки x=y=0 имеем:
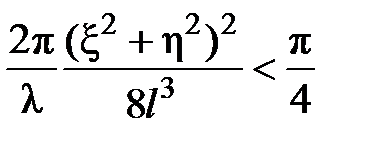 . (7.39)
. (7.39)
Отсюда получаем, что дифракционный интеграл Френеля даёт результаты с достаточной точностью, если расстояние  до плоскости
до плоскости  удовлетворяет неравенству:
удовлетворяет неравенству:
 ,
,
где  – максимальный радиус отверстия.
– максимальный радиус отверстия.
Если в интеграле (7.38) можно пренебречь членом  , то получится соотношение
, то получится соотношение
 , (7.40)
, (7.40)
которое называется дифракционным интегралом Фраунгофера. В этом интеграле обозначено:
 .
.
Определим область применимости интеграла Фраунгофера.
Используя условие (7.39), получим
 .
.
Следовательно, интеграл (7.40) можно использовать на расстояниях

Эти расстояния в 4 и более раз превосходят дифракционную длину светового пучка, т.е. удовлетворяют условию дальней зоны дифракции.
Приведём численную оценку  и
и  . При
. При  мм и
мм и 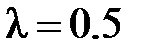 мкм находим
мкм находим  =300 мм и
=300 мм и  =800 м.
=800 м.
Рис. 7.19 Области использования интегралов Кирхгофа, Френеля и Фраунгофера
Наглядное представление областей применимости использования интегралов Кирхгофа, Френеля и Фраунгофера для расчёта дифракционных полей даёт рисунок 7.19. Видно, что интеграл Кирхгофа в принципе можно использовать в диапазоне  непосредственно от диафрагмы до бесконечности. Однако, чтобы не возникало больших вычислительных затрат и погрешностей, разумная зона его применения должна быть ограничена диапазоном
непосредственно от диафрагмы до бесконечности. Однако, чтобы не возникало больших вычислительных затрат и погрешностей, разумная зона его применения должна быть ограничена диапазоном  По тем же причинам интеграл Френеля следует использовать в диапазоне
По тем же причинам интеграл Френеля следует использовать в диапазоне  , а интеграл Фраунгофера – в дальней зоне дифракции.
, а интеграл Фраунгофера – в дальней зоне дифракции.
Приведённые значения  и
и  получены для случая падения на диафрагму плоской световой волны. В тех случаях, когда фронт волны на отверстии диафрагмы сходящийся, можно считать, что он образован идеальной линзой и источником излучения является некоторая точка
получены для случая падения на диафрагму плоской световой волны. В тех случаях, когда фронт волны на отверстии диафрагмы сходящийся, можно считать, что он образован идеальной линзой и источником излучения является некоторая точка  в предметной плоскости (рис. 7.20). В этом случае т.
в предметной плоскости (рис. 7.20). В этом случае т.  , являющаяся изображением т.
, являющаяся изображением т.  , представляет собой дифракционное изображение в области дифракции Фраунгофера. (Если т.
, представляет собой дифракционное изображение в области дифракции Фраунгофера. (Если т.  находится в бесконечности, то т.
находится в бесконечности, то т.  совпадает с задним фокусом линзы). В этом случае угловые переменные
совпадает с задним фокусом линзы). В этом случае угловые переменные  в интеграле Фраунгофера (7.40) следует определять по формулам
в интеграле Фраунгофера (7.40) следует определять по формулам
 ,
,  .
.
Рис. 7.20 Определение области дифракции Фраунгофера для сходящейся волны
Областью дифракции Фраунгофера следует считать область  окрестности т.
окрестности т.  , из которой на световом диаметре
, из которой на световом диаметре  линзы укладывается меньше половины первой зоны Френеля. Следовательно, разность стрелок прогиба с центрами в точках P и В (границы этой области) на световом диаметре должна быть равной
линзы укладывается меньше половины первой зоны Френеля. Следовательно, разность стрелок прогиба с центрами в точках P и В (границы этой области) на световом диаметре должна быть равной 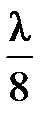 , т.е.
, т.е.
 . (7.41)
. (7.41)
Решение уравнения (7.41) относительно  при условии
при условии  имеет вид:
имеет вид:
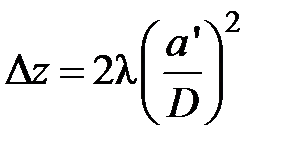 (7.42)
(7.42)
Если предметная плоскость находится в бесконечности, то  и тогда:
и тогда:
 , (7.43)
, (7.43)
где  – диафрагменное число линзы.
– диафрагменное число линзы.
Отрезок  , определяемый соотношениями (7.42) и (7.43), называют дифракционной глубиной резкого изображения. Она должна учитываться конструкторами при расчёте допусков на установку прицельных сеток и регистраторов изображения. На практике именно плоскость изображения представляет для разработчиков оптических приборов наибольший интерес. Поэтому с точки зрения определения качества изображения особое внимание следует уделить дифракции Фраунгофера.
, определяемый соотношениями (7.42) и (7.43), называют дифракционной глубиной резкого изображения. Она должна учитываться конструкторами при расчёте допусков на установку прицельных сеток и регистраторов изображения. На практике именно плоскость изображения представляет для разработчиков оптических приборов наибольший интерес. Поэтому с точки зрения определения качества изображения особое внимание следует уделить дифракции Фраунгофера.
Представим дифракционный интеграл (7.40) в виде:
 .
.
Известно, что интегральное преобразование функции  вида:
вида:

называется двумерным преобразованием Фурье, поэтому дифракцию Фраунгофера в плоскости изображения с точностью до постоянной С можно считать преобразованием Фурье от функции, описывающей распределение поля в выходном зрачке оптической системы, т.е.
 ,
,
где
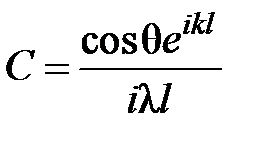 ,
,  .
.
Примечания:
1. Если точки  и
и  находятся на оси z, то следует принять:
находятся на оси z, то следует принять: 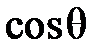 = 1, l=L; в частности, для изображающей системы получаем:
= 1, l=L; в частности, для изображающей системы получаем:
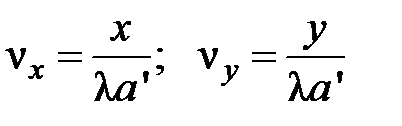
а для задней фокальной плоскости объектива –

2. Если углы дифракции малые, то можно принять
 ,
,  .
.
 2020-04-12
2020-04-12 2067
2067








