Экспоненциальное (показательное) распределение

Случайная величина х распределена по экспоненциальному закону, если плотность распределения вероятности имеет вид

, (16)

где х – случайная величина, – постоянная.

Если за случайную величину принять время работы до отказа изделия то выражение для плотности вероятности можно переписать в следующем виде:

, (17)

где t – время работы до отказа, − интенсивность отказов.

Для характеристик непрерывных распределений используется функция распределения :

. (18)

Подставив сюда выражение для плотности вероятности (2.21), получим значение функции распределения для экспоненциального закона:

. (19)

Физический смысл функции распределения – это вероятность того, что случайная величина попадает в интервал от 0 до t.

Экспоненциальный закон распределения характеризуется математическим ожиданием (среднее время наработки на отказ)

. (20)

Экспоненциальный закон применяется только в тех случаях, когда наблюдается незначительный сбой в работе изделия, а отказы распределены равномерно в равных интервалах времени.

Обычно с помощью этого закона описывают: продолжительность обслуживания покупателя, время жизни оборудования до отказа, промежуток времени между поломками и т.п.

Функция, которая задаёт закон распределения непрерывной случайной величины или функция распределения:

Функция плотности распределения:

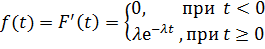
Функцией надежности R(t), называют функцию, определяющую вероятность безотказной работы элемента за время длительностью t:

R(t) = P(T > t) = 1 – F(t) (21)

Пример 10

Время безотказной работы устройства распределено по показательному закону f(t) = 0,02e^-0,02t при t ≥ 0 (t – время в часах). Какова вероятность того, что устройство проработает безотказно 50 часов?

Решение.

По условию постоянная интенсивность отказов

λ = 0,02. Используя формулы (19,21), получаем:

R(50) = e^-0,02·50 = e^-1 ≈ 0,368.

Формула Пуассона

Формулу Пуассона можно считать математической моделью простейшего потока событий:

(21)

Вероятность появления k событий за промежуток времени, равный t, − интенсивность потока событий.

Пример 11.

Среднее число вызовов, поступающих на АТС в одну минуту, равно 2. Найти вероятность того, что за 5 минут поступит а) 2 вызова; б) менее двух вызовов; в) не менее двух вызовов.

Поток вызовов предполагается простейшим.

Решение.

По условию 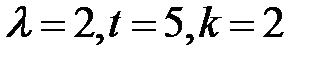, воспользуемся формулой Пуассона.

а) искомая вероятность того, что за 5 минут поступит 2 вызова

Это событие практически невозможно

б) Событие «не поступило ни одного вызова» и «поступил один вызов» несовместны, поэтому по теореме сложения искомая вероятность того, что за 5 минут поступит менее двух вызовов, равна

Это событие практически невозможно.

в) События «поступило менее двух вызовов» и «поступило не менее двух вызовов» противоположны, поэтому искомая вероятность того, что за 5 минут поступит не менее двух вызовов.