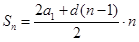Теоретический справочник

Определение: Последовательность 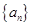, у которой задан первый член a₁, а каждый следующий равен предыдущему, сложенному с одним и тем же числом d, называется арифметической прогрессией: a_n+1 = a_n + d, где d - разность прогрессии.

• Если d> 0, то прогрессия является возрастающей. Если d <0, то прогрессия является убывающей.
• Арифметическая прогрессия считается конечной, если рассматриваются только ее первые несколько членов.

Формулы арифметической прогрессии:

• a_n = a₁ + d (n - 1) - формула n- го члена арифметической прогрессии;
• 2a_n = a_{n - 1} + a_{n + 1} - характеристическое свойство арифметической прогрессии для трех последовательных чисел;
• 2a_n = a_{n - k} + a_{n + k,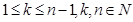}  - характеристическое свойство арифметической прогрессии двух равноотстоящих от третьего члена прогрессии;
• a_n = a_k + d (n - k) - формула нахождения n- го члена арифметической прогрессии через k -ый член прогрессии;
• a_n + a_m = a_k + a_l, - характеристическое свойство арифметической прогрессии для четырех произвольных чисел, если n + m = k + l.

Сумма n членов арифметической прогрессии:

Геометрическая прогрессия»

Теоретический справочник

Определение. Последовательность , у которой задан первый член 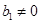, а каждый следующий равен предыдущему, умноженному на одно и то же число 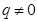, называется геометрической прогрессией: 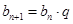, где q - знаменатель прогрессии

• Если | q |> 1, то прогрессия называется возрастающей. Если | q | <1, то прогрессия называется убывающей.
• Геометрическая прогрессия считается конечной, если рассматриваются только ее первые несколько членов.
• Пусть (х_п)— геометрическая прогрессия со знаменателем q, где | q | <1 и q≠ 0. Суммой бес­конечной геометрической прогрессии, знаменатель которой удовлетворяет условию | q |<1, называется предел суммы n первых ее членов при n→∞.