2020-04-12
201
В результате замены в разностном уравнении входного сигнала на единичный дискретный импульс 
, получим выражение для импульсной характеристики нерекурсивной ЛДС:
или
. (6.7)
Соответственно, передаточная функция ЛДС с конечной импульсной характеристикой имеет следующий вид:
. (6.8)
Таким образом:
- импульсная характеристика нерекурсивной ЛДС имеет конечную длительность, а отсчеты импульсной характеристики равны коэффициентам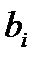 
разностного уравнения;
- нерекурсивные ЛДС называют системами с конечной импульсной характеристикой (КИХ, finite impulse response – FIR);
- передаточная характеристика нерекурсивной ЛДС не имеет полюсов;
- вследствие отсутствия обратных связей и полюсов любой нерекурсивный фильтр является устойчивым.
Достоинства нерекурсивных ЛДС:
- возможность получения линейных фазочастотных характеристик;
- абсолютная устойчивость.
Недостатки нерекурсивных ЛДС: для получения частотных характеристик с высокой прямоугольностью АЧХ необходимы фильтры высокого порядка.
Импульсная характеристика рекурсивного фильтра описывается бесконечными степенными рядами:
. (6.9)
где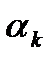 
- полюс;
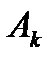- коэффициент разложения при k-м полюсе.
Передаточная функция рекурсивной ЛДС описывается передаточной функцией общего вида:
. (6.10)
Таким образом:
- наличие в рекурсивном фильтре обратных связей позволяет получить бесконечную импульсную характеристику;
- рекурсивные фильтры также называются фильтрами с бесконечной импульсной характеристикой (БИХ, infinite impulse response – IIR);
- передаточная функция рекурсивных фильтров всегда имеет полюса;
- из-за наличия обратных связей и полюсов рекурсивные фильтры могут быть неустойчивыми.
Достоинством рекурсивных фильтров является высокая крутизна спадов АЧХ даже при малом порядке фильтра.
Недостатком рекурсивных фильтров является нелинейность фазочастотной характеристики.
