2020-04-12
106
Задачи позволяют проверить умения студента применять математический аппарат для оценивания стабильности технологических процессов и рассчитывать границы контрольных карт по количественному и альтернативному признакам регулирования.
Задача 5.1
Оценивание доли несоответствующей продукции по индексам технологического процесса
Возможности технологического процесса характеризуются индексом С р = 1,33 и индексом С рк = 1. Предполагается, что разброс параметров изделий подчиняется нормальному распределению.
Определить долю брака (несоответствующей продукции). Оценить, насколько уменьшится доля брака, если удастся практически полностью отцентрировать процесс.
Решение
По определению индексы вычисляются по формулам
; 
либо 
,
где 
и 
– верхняя и нижняя границы допуска; 
и 
– среднее квадратическое отклонение и среднее значение (оценка математического ожидания) контролируемых параметров изделия.
Построим график нормального закона распределения в поле допуск [ х в; х н] для заданных значений С р и С рк. . Для этого выразим границы поля допуска и среднее значение через среднее квадратическое отклонение. Из формулы для индекса С р получим ширину допуска
|
|
|
.
Для симметричного допуска
; 
.
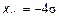Из формулы для индекса 
найдем среднее значение
.
Если воспользоваться второй формулой, то 
.
По полученным расчетным данным строят плотность распределения контролируемого параметра (рисунок 5.1).
Рисунок 5.1 – Плотность распределения контролируемого параметра
и границы допуска
Доля брака определяется вероятностью
,
где Ф(.) – функция нормального распределения нормированной случайной величины; 
и 
– нормированные переменные.
Для рассматриваемого случая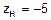 
и 
. Тогда искомая вероятность будет равна
.
Если рассматривать смещение среднего в другую сторону, т. е.
,
то нормированные переменные для нашего примера будут равны z н= = 
и z в= 5. В силу симметрии результат аналогичен: 
.
В процессе отладки технологического процесса стремятся уменьшить значение 
до нуля, т. е. 
= 0 (см. пунктир на рисунке 5.1). Тогда индекс 
поднимается до значения 1,33 и 
.
Следовательно, доля брака
т. е. 0,006%, или 60 ppm.
Процент брака уменьшился в 20 раз.
Действительно, цифра 0,00006 соответствует вероятности выхода случайной величины за границы ±4s для нормального закона распределения.
Задача 5.2
