2020-04-12
403
Рассчитать предупредительные границы и границы регулирования для 
- карты (карты средних значений) для контроля технологической операции изготовления детали заданного диаметра. Известно, что процесс стабилен и характеризуется по предыдущим контрольным данным средним значением диаметра 
мм и выборочной оценкой среднего квадратического отклонения 
мм.
Уровень значимости для предупреждающих границ – 0,025, для границ регулирования – 0,001.
Решение
Среднее значение параметра в одной j -й выборке вычисляется по формуле
,
где xi – измеренные парметры в данной выборке; n – объем выборки.
Выберем n = 5, так как уже при таком объеме закон распределения средних значений достаточно близок к нормальному.
Границы контрольной карты средних значений определяются выражением
где 
– среднее значение средних арифметических контролируемого параметра, полученное за длительный предыдущий интервал; 
– верхняя граница; 
– нижняя граница; z – нормированный квантиль порядка (1-α) нормального распределения; α – уровень значимости (0,025 или 0,001); n – объем одной выборки; σ – среднее квадратическое значение контролируемого процесса.
По таблице нормального распределения для предупреждающих границ (1–αп = 0,975) находим квантиль z п = 1,96 и для границ регулирования (1–αр = 0,999) квантиль z р = 3,1.
Среднее квадратическое значение s не известно, а известна лишь выборочная его средняя оценка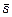 
(
, где 
среднее квадратическое отклонение одной выборки предыдущего контроля, к – число выборок), поэтому использование в формуле для расчета границ выборочной оценки дает смещенный результат.
Воспользуемся поправочным коэффициентом 
для получения несмещенной оценки
.
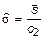Коэффициент с 2 стремится к единице при увеличении объема выборки. Значение коэффициента с 2 можно найти в таблицах справочников по статистическим расчетам либо рассчитать по формуле
,
где Г – гамма-функция, которая табулирована и приводится в литературе.
Подставляя в формулу значение n = 5, получим:
.
Вычислим значения гамма-функций. По известным правилам математики
;
.
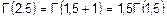По таблице гамма-функции находим
и 
.
Тогда искомый коэффициент будет равен:
.
Следовательно, несмещенная оценка среднего квадратического отклонения
мм.
Таким образом, верхняя и нижняя предупреждающие границы карты средних будут равны
мм.
мм.
Верхняя и нижняя границы регулирования
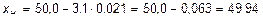мм.
мм.
Задача 5.3
Определение параметров np -карты альтернативного
контроля
Рассчитать границы регулирования np -карты, если известно, что объем выборки постоянный, а средняя доля дефектных изделий 
Границы должны соответствовать уровню значимости 
.
Решение
Верхняя и нижняя границы регулирования по числу дефектов в выборке при известной средней доле дефектных изделий в партии определяются по формуле
,
где n – объем выборки; 
– средняя доля дефектных изделий в партии; z – нормированный квантиль порядка 
нормального распределения; σ – среднее квадратическое отклонение.
Определим величины, недостающие для расчета по приведенной формуле.
Объем выборки находим, воспользовавшись формулой биноминального распределения, которая определяет вероятность обнаружения среди n взятых из партии изделий точно k бракованных
,
где Р – вероятность; x – число дефектных изделий в выборке; k – заданное число; n – объем выборки; p – доля дефектных изделий в партии; 
– число сочетаний из n по k.
Оптимальный объем выборки находится при условии k = 0, что соответствует принятию за нижнюю границу числа дефектных изделий в выборке, равного нулю.
Исходя из заданного уровня значимости 
. Тогда 
,
откуда следует
Следовательно, оптимальный объем выборки
Квантиль порядка (1– 0,005 = 0,995) определим из таблицы нормального распределения 
. Так как задано 
, то z = 2,57.
Верхняя граница регулирования (или максимально допустимое число дефектных изделий в выборке) равна
.
Так как число дефектных изделий может быть только целым, и чтобы избежать неопределенности в принятии решения, установим верхнюю границу np -карты, равную 
.
Нижняя граница регулирования
.
Получено отрицательное число, следовательно, принимаем 
, что соответствует условию, при котором рассчитывался оптимальный объем выборки.
Наиболее употребительные обозначения
– истинное значение абсолютной погрешности
– действительное значение абсолютной погрешности
– пределы допускаемой абсолютной погрешности
– действительное значение относительной погрешности
– пределы допускаемой относительной погрешности
– пределы допускаемой приведенной погрешности
х – входная (измеряемая) величина
y – выходная величина измерительного преобразователя
S – чувствительность линейного измерительного звена
– показания измерительного прибора
q – ступень квантования цифрового измерительного прибора
sign – знак
Ent – целая часть
Р – вероятность
f (·) – плотность вероятности
F (·) – функция распределения
m – математическое ожидание
– среднее квадратическое отклонение
Ф и Ф0 – нормированные функции нормального распределе-
ния (Ф = 0,5±Ф0)
– нормированная центрированная переменная
Список литературы
1 Новицкий П. В., Зограф И. А. Оценка погрешностей результатов измерений. – Л.: Энергоатомиздат, 1991. – 304 с.
2 Поверка средств электрических измерений: Справочная книга / Л. И. Любимов, И. Д. Форсилова, Е. З. Шапиро. – Л.: Энергоатомиздат, 1987. – 296 с.
3 Маркин Н. С. Практикум по метрологии: Учеб. пособие. – М.: Изд-во стандартов, 1994. – 188 с.
4 Практикум по вероятностным методам в измерительной технике: Учеб. пособие/ В. В. Алексеев, Р. В. Долидзе, Д. Д. Недосекин,
Е. А. Чернавский. – СПб: Энергоатомиздат, Санкт-Петербургское отделение, 1993. – 264 с.
5 Метрологические испытания измерительных приборов и мер электрических величин: Метод. указ. к выполнению лабораторных работ / Г. П. Шлыков, К. В. Сафронова, А. А. Данилов; Под ред.
Г. П. Шлыкова. – Пенза: Изд-во Пенз. гос. техн. ун-та, 1996. – 84 с.
6 Журавин Л. Г., Семенов Е. И., Шлыков Г. П. Расчет метрологических характеристик при проектировании средств измерений: Учеб. пособие/Под ред. Г. П. Шлыкова. – Пенза: Пенз. политехн. ин-т, 1988. – 80 с.
7 Шлыков Г. П. Функциональный и метрологический анализ средств измерений и контроля: Учеб. пособие. Ч. 1. – Пенза: Изд-во Пенз. гос. техн. ун-та, 1998. – 94 с.
8 Шлыков Г. П., Брагин А. А., Семенюк А. Л. Методы и средства метрологических испытаний аналого-цифровых измерительных устройств: Учеб. пособие/Под. ред. Г. П. Шлыкова. – Пенза: Пенз. политехн. ин-т, 1990. – 76 с.
9 Мердок Дж. Контрольные карты/Перевод с англ. – М.: Финансы и статистика, 1986. – 151 с.
10 Справочник по вероятностным расчетам / Г. Г. Абезгауз,
А. П. Тролев, Ю. Н. Коленкин, И. А. Коровина. – М.: Воениздат, 1970. – 536 с.
11 Чекмарев А. Н., Барвинок В. А., Шалавин В. В. Статистические методы управления качеством. – М.: Машиностроение, 1999. – 320 с.
Приложение А
Классы точности средств измерений
По ГОСТ 8.401–80 «ГСИ. Классы точности средств измерений. Общие требования» пределы допускаемых погрешностей определяются симметричными границами следующим образом.
В форме абсолютных погрешностей нормируют двумя способами
или 
,
где 
– пределы допускаемой абсолютной основной погрешности, выраженной в единицах измеряемой величины; a и b – положительные числа (a – размерное и b – безразмерное); x – значение измеренной величины.
В форме относительных погрешностей нормируют следующими способами:
или 
,
где 
– пределы допускаемой относительной основной погрешности, выраженные в процентах; q, c, d – положительные безразмерные числа, выбираемые из ряда, установленного стандартом; 
– нормирующее (часто конечное) значение диапазона измерений.
В форме приведенной погрешности нормируют в виде
,
где – пределы допускаемой приведенной основной погрешности, выраженные в процентах; p – положительное число, выбираемое из ряда, установленного стандартом.
Приложение Б
Оценивание предельных погрешностей функций
Для функции двух и более аргументов y = f (x 1; х 2; …; хn)
предельная абсолютная погрешность функции в заданной точке
(x 1; х 2; …; хn) определяется по формуле
,
где 
– модули частных производных, вычисленных в точке (x 1; х 2;... … хn); n – число аргументов; D хi – предельные погрешности аргументов хi.
Предельная относительная погрешность функции
,
где d х i – предельные погрешности аргументов х i .
Для n > 3 применяют формулу геометрического сложения
.
Формулы предельных погрешностей простейших функций приведены в таблице.
| Функция | Абсолютная погрешность | Относительная погрешность |
| 
| 
|
| 
| 
|
| 
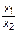
| d x 1+d x 2 |
| ax | a D x | d x |
| xn | n xn- 1D x | n d x |
Приложение В
Значения функции нормального распределения (интеграл Лапласа–Гаусса)
.
где 
; m – математическое ожидание; s – среднее квадратическое отклонение.
Основные свойства
0,5 + Ф0(z), если z ≥ 0;
Ф(z) = Ф0(– z) = – Ф0(z).
0,5 – Ф0(z), если z < 0.
| z | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8 1,9 2,0 2,1 2,2 2,3 2,4 2,5 2,6 2,7 2,8 2,9 3,0 4,0 4,5 | 0,0000 0398 0793 1179 1554 1915 2257 2580 2881 3159 3413 3643 3849 4032 4192 4332 4452 4554 4641 4713 4772 4821 4861 4893 4918 4938 4953 4965 4974 4981 49865 499968 499997 | 0,0004 0438 0832 1217 1591 1950 2291 2611 2910 3186 3438 3665 3869 4049 4207 4345 4463 4564 4649 4719 4778 4826 4864 4896 4920 4940 4955 4966 4975 4982 49903 | 0,0080 0478 0871 1255 1628 1985 2324 2642 2939 3212 3461 3686 3888 4066 4222 4357 4474 4573 4656 4726 4783 4830 4868 4898 4922 4941 4956 4967 4976 4982 49931 | 0,0120 0517 0910 1293 1664 2019 2357 2673 2967 3238 3485 3708 3907 4082 4236 4370 4484 4582 4664 4732 4788 4834 4871 4901 4925 4943 4957 4968 4977 4983 49952 | 0,0160 0557 0948 1331 1700 2054 2389 2703 2995 3264 3508 3729 3925 4099 4251 4382 4495 4591 4671 4738 4793 4838 4874 4904 4927 4945 4959 4969 4977 4984 49966 | 0,0199 0596 0987 1368 1736 2088 2422 2734 3023 3289 3531 3749 3944 4115 4265 4394 4505 4599 4678 4744 4798 4842 4878 4906 4929 4946 4960 4970 4978 4984 49977 | 0,0239 0636 1026 1406 1772 2123 2454 2764 3051 3315 3554 3770 3962 4131 4279 4406 4515 4608 4686 4750 4803 4846 4881 4909 4931 4948 4961 4971 4979 4985 49984 | 0,0279 0675 1064 1443 1808 2157 2486 2794 3078 3340 3577 3790 3980 4147 4292 4418 4525 4616 4693 4756 4808 4850 4884 4911 4932 4949 4962 4972 4979 4985 49989 | 0,0319 0714 1103 1480 1844 2190 2517 2823 3106 3365 3599 3810 3997 4162 4306 4429 4535 4625 4699 4761 4813 4854 4887 4913 4934 4951 4963 4973 4980 4986 49993 | 0,0359 0753 1141 1517 1879 2224 2549 2852 3133 3389 3621 3830 4015 4177 4319 4441 4545 4633 4706 4767 4817 4857 4890 4916 4936 4952 4964 4974 4981 4986 49995 |
Приложение Г
Тесты и задачи по учебным дисциплинам
Приложение Г.1
Тесты и задачи по дисциплине "Метрология" (с ответами)
|
| Шкала наименования Шкала классификации Порядковая шкала Интервальная шкала Шкала отношений | o o o x o | ||||||
| 2 Перечислите основные операции любого процесса измерения | 1 Воспроизведение физической величины заданного размера 2 Сравнение величин 3 Масштабирование 4 Формирование результата | |||||||
|
| Случайная Абсолютная Приведенная Аддитивная Относительная Субъективная | – o x x – o x – o | ||||||
| 4 Напишите формулы для расчета погрешностей функций по заданным погрешностям аргументов | ||||||||
| y = S (x 1 +x 2) y = S·x 1 ·x 2 ·x 3 y = S·xn | Δ y = S (Δ1 +Δ2) δ y = δ1+ δ2 + δ3 Δ y = S (n xn- 1+Δ X); δ = n ·δ x | |||||||
| 5 Электрическая мощность измеряется косвенным методом путем поочередного измерения сопротивления R нагрузки и тока I через нагрузку. Результат определяют по формуле P = I 2 R. Напишите выражение для расчета предельной относительной погрешности измерения мощности δ Р по известным предельным относительным погрешностям измерения сопротивления δ R и измерения тока δ I |
| |||||||
|
| 2 o 3 o 4 x 5 x 6 x | |||||||
| 7 По результатам эксперимента получена зависимость ε y = f (x) абсолютной погрешности измерительного устройства (приведенная к выходу) от значения измеряемой величины х
Определите аддитивную погрешность εадд, приведенную к выходу, мультипликативную погрешность η и максимальную нелинейную составляющую погрешности εнел, приведенную к выходу, если номинальная чувствительность S = 100 Гц/В | ||||||||
|
εадд= –2 Гц; η=
| ||||||||
|
| Мультипликативной погрешностью Погрешностью сравнения Массой и габаритными размерами Гистерезисом Временной реакцией Значением напряжения электропитания | o x o x x o | ||||||
1 К какому типу шкал относится шкала времени?
, или 8%; εнел=1,5 Гц
| 9 Запишите общую функцию преобразования y = f (x) трех цепей линейных звеньев (S – чувствительность) | ||
|
|
y = S 1 S 2 x
y = (S 1+ S 2 ) x
 при S 1 S 2>>1
| |
| 10 Составьте метрологическую модель линейного безынерционного звена | ||
|
| ||
| 11 Определите предельные значения аддитивной погрешности цепи линейных звеньев, приведенной ко входу | ||
|
| 
| |
| 12 Составьте структурную метрологическую модель источника опорного напряжения U 0 компенсационного типа, построенного по схеме: | ||
U – питание;
У – усилитель;
E ст – напряжение параметрического стабилизатора
|
dст – погрешность напряжения параметрического стабилизатора; dдн – погрешность коэффициента деления делителя; Dус – погрешность нуля усилителя; dус – погрешность коэффициента усиления (практически не влияет); S дн – коэффициент деления делителя (в обратной связи) | |
и к выходу 
Ом/°С; 
В/Ом; 
;
0,5 °С; 
Ом; 
мВ
Приложение Г.2
Тесты и задачи по дисциплине "Метрологическое обеспечение средств измерений" (с ответами)
| 1 При сличении показаний поверяемого и образцового приборов оказалось, что они отличаются на |
| ||||||||
| 2 Вольтметр поверяется методом непосредственного сличения с показанием образцового вольтметра. Влияют ли на результат поверки характеристики источника регулируемого напряжения, которое измеряют оба вольтметра? | |||||||||
|
| Может влиять Не влияет | o x | |||||||
|
| Может влиять Не влияет | o x | |||||||
|
| Может влиять Не влияет | x o | |||||||
| 3 В каких точках диапазона измерений при поверке определяют действительные значения погрешностей магнитоэлектрического прибора – в оцифрованных отметках цифрового частотомера – в конце диапазона (варианты: во всех точках, в начале и конце диапазона, в начале, середине и конце диапазона, в оцифрованных отметках или другие) | |||||||||
| 4 Пределы допускаемой погрешности поверяемого и образцового омметров соответственно равны 0,1 и 0,02 Ом. Какой контрольный допуск необходимо установить, чтобы риск 2 рода (риск потребителя, риск хозяина поверяемого прибора) был равен нулю? | 0,1–0,02 =0,08 Ом | ||||||||
| 5 Изобразите схему установки для поверки измерительного преобразователя с помощью образцового преобразователя и образцового компаратора |
| ||||||||
  6 Межповерочный интервал рабочих средств измерений устанавливает
| Госстандарт Завод-изготовитель Метрологическая служба предприятия | o o x | |||||||
| 7 Амперметр поверяется в конечной точке диапазона путем измерения образцовым вольтметром напряжения на образцовом резисторе. Какими предельными относительными погрешностями должны обладать образцовые средства, если приведенная погрешность амперметра | (0,5–0,4)/2 =0,05% | ||||||||
| 8 Право поверки средств измерений на предприятии дается | директором предприятия директором ЦСМС Госстандартом РФ Органом гос. метрологической службы Госстандартом на основании акта гос. метрологической службы | o o o o x | |||||||
|
| нормальный равномерный трапециевидный Симпсона Рэлея | o x o o o | |||||||
|
| списывают прибор отправляют в ремонт сообщают владельцу о факте сообщают владельцу о факте и о действительном значении погрешности | o o o x | |||||||
=0,83
Нестабильность за время поверки
0,5%, а установленный контрольный допуск 0,4% (для риска потребителя, равного нулю)?
10 Если измерительный прибор во время поверки был признан метрологически непригодным, то
Приложение Г.3
Тесты и задачи по дисциплине "Методы и средства измерений
электрических величин" (с ответами)
|
| магнитоэлектрической электромагнитной электродинамической электростатической | o x x x | |
|
| среднего действующего средневыпрямленного амплитудного | o x o o | |
 3 При измерении напряжения погрешность от несогласования «объект-прибор» вызвана…
| низким входным сопротивлением вольтметра низкой чувствительностью высокой чувствительностью большим выходным сопротивлением источника измеряемого напряжения (объекта) соотношением сопротивлений объекта | o o o o x | |
| 4 Погрешность прибора нормируется приведенной погрешностью |
| ||
| 5 Напишите формулу нормирования погрешности прибора, если его класс точности обозначен 0,1/0,05 |
| ||
|
| погрешность менее 0,01% требований к точности нет стабильность значение напряжения не должно быть меньше рассчитанного значения | o o o x | |
. Какова относительная погрешность измерения, если измеряемое напряжение оказалось равным 0,5 (и 0,25) от предела измерений?
|
| резистор индуктивность конденсатор | o o x | |||
|
| "детектор-усилитель" 1 аттенюатор 2 детектор 3 усилитель постоянного тока 4 магнитоэлектрический прибор | ||||
| "усилитель-детектор" 1 аттенюатор 2 усилитель переменного тока 3 детектор 4 магнитоэлектрический прибор | |||||
  9 Операции квантования по уровню присущи …
| электромеханическим измерительным приборам аналоговым электронным приборам цифровым приборам | o o x | |||
| 10 Цифровой метод измерения среднего значения частоты электрического сигнала заключается в …
| подсчете числа периодов измеряемого сигнала за образцовый интервал времени подсчете числа периодов образцовой частоты за период измеряемого сигнала |
x
o | |||
| 11 Электронный осциллограф используется для …
| наблюдения формы сигналов измерения временных параметров сигналов измерения электрического сопротивления измерения амплитуды переменных сигналов все вместе | x x o x o | |||
| 12 Два полных периода исследуемого сигнала видны на экране осциллографа, если период развертывающего напряжения …
| в два раза меньше периода исследуемого сигнала равен периоду исследуемого сигнала в два раза больше периода исследуемого сигнала | o o x | |||
8 Обозначьте наименования узлов электронных вольтметров типа “детектор-усилитель” и “усилитель-детектор”
Приложение Г.4
Тесты и задачи по дисциплине
"Методы и приборы контроля качества" (с ответами)
|
| входной измерительный операционный допусковый приемочный неразрушающий | o x o x o | |||||||
  2 Результатом контроля единицы продукции является…
| значение контролируемого параметра интервал, в котором находится истинное значение контролируемого параметра решение о принадлежности к определенной совокупности | o o x | |||||||
| 3 Вероятность ошибки второго рода при контроле – это …
| вероятность ошибочной приемки бракованного изделия вероятность ошибочной браковки годного изделия вероятность выхода контролируемого параметра за поле допуска | x o o | |||||||
|
| значение предельно допускаемой абсолютной погрешности контроля половину значения предельно допускаемой абсолютной погрешности контроля удвоенное значение предельно допускаемой абсолютной погрешности контроля | o o x | |||||||
|
| риск изготовителя риск потребителя доля годных изделий доля забракованных изделий | x o o x | |||||||
|
| ограниченность выборки погрешность средств контроля совместное действие указанных факторов | o o x | |||||||
|
| малозначительным значительным критическим | o x o | |||||||
|
| сплошной выборочный выборочный при малом значении риска потребителя | o o x | |||||||
|
| резонансный эхо-импульсный теневой свободных колебаний акустической эмиссии | o o o o x | |||||||
|
| резонансный эхо-импульсный теневой свободных колебаний акустической эмиссии | x o o o o | |||||||
|
| эхо-импульсный акустический теневой акустический вихретоковый магнитопорошковый капиллярный | o x x o o | |||||||
|
| вихретоковые ультразвуковые магнитные | o x o | |||||||
|
| минимальный размер обнаруживаемого дефекта минимальная глубина залегания дефекта минимальное расстояние между двумя дефектами, расположенными на вертикальной оси минимальное расстояние между двумя дефектами, расположенными на одной глубине | o o x o | |||||||
|
| вихретоковые ультразвуковые магнитные | o o x | |||||||
|
| дефектоскопы эндоскопы стуктуроскопы | o x o | |||||||
|
| продольное циркулярное комбинированное | o x o | |||||||
|
| масс-спектрометрический галогенный электронозахватный | x o o | |||||||
|
| капиллярные магнитные вихретоковые тепловые | x o x o | |||||||
|
| содовым раствором легколетучими растворителями керосином металлической щеткой | x x o o | |||||||
|
| вихретокового структуроскопа магнитного (феррозондового) структуроскопа тепловизора | o x o | |||||||
13 Разрешающая способность по дальности эхо-импульсного дефектоскопа – это …
14 Для контроля толщины немагнитных непроводящих покрытий на изделиях из ферромагнитных материалов используют толщиномеры …Приложение Г.5
Тесты и задачи по дисциплине
"Статистические методы управления качеством" (с ответами)
| 1 Приведите пример построения диаграммы Парето для выявления приоритетов |
| |||||||||
|
| 4,5% 0,27% 0,006% 0,0006% | o o x o | ||||||||
| 3 Разброс погрешностей емкости конденсаторов при их массовом производстве характеризуется законом распределения, который аппроксимируется несимметричным треугольником с границами –15% и +35%. Определите, какой процент конденсаторов оказывается годными, если установлен несимметричный допуск (–10; +20)% | нормирование: АО=0,04
| |||||||||
| 4 Предприятие получило с завода-изготовителя партию резисторов. По результатам входного контроля была построена гистограмма погрешностей. Какой вывод можно сделать, анализируя характер (вид) гистограммы? | ||||||||||
|
| На заводе-изготовителе произведена разбраковка. Наиболее точные резисторы включены в другую партию. Автомат, разбраковывающий резисторы, имеет погрешность смещения | |||||||||
|
| n /10
5 lg n
| o x o | ||||||||
  6 Какие типы контрольных карт применяют при альтернативном контроле продукции?
| Средних Медиан Дисперсий s Доли несоответствующей продукции p Числа дефектов в группе c Числа дефектов на единицу и | o o o x x x | ||||||||
| 7 Верхняя UCL и нижняя LCL контрольные границы карты средних устанавливаются по формуле
|
А – | среднее значение средних среднее значение средних квадратических отклонений коэффициент, определяющийся заданной вероятностью | ||||||||
|
| равномерного Пуассона нормального хи - квадрат | o o x o | ||||||||
|
| число годных изделий в выборке допускаемое число бракованных изделий в выборке допускаемое число бракованных изделий в партии | o x o | ||||||||
| 10 По известной оперативной характеристике (P г(p) – вероятность принятия партии от числа дефектных изделий) одноступенчатого плана выборочного контроля при приемке партии изделий определите риск изготовителя
|
| |||||||||
), определяется по формуле
. Расшифруйте формулу
–
–
9 Приемочное число выборочного контроля изделий при приеме партии – это …
и риск потребителя 
, если приемочный уровень 
=0,01, а браковочный уровень 
=0,04
Приложение Д
Билеты междисциплинарного экзамена
Приложение Д.1
Междисциплинарный экзамен для студентов,
обучающихся по специальности 0720
БИЛЕТ № 1-С
1 Решите задачи
1.1 ОТК проверяет среднее квадратическое значение U уровня шумов на выходе электронного усилителя. Экземпляр усилителя был забракован, так как измеренное значение  превышает допускаемую границу Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:
Сейчас читают про:
  6007 5776 |
