Статистическое распределение выборки

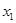    Пусть из генеральной совокупности извлечена выборка объема . Причем объект  наблюдался  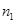раз; -  раз;… -  раз. Причем  - объем выборки.

    Опр. 6 Наблюдаемые значения   называются вариантами, а последовательность вариант записанных в возрастающем порядке – вариационным рядом.

    Опр. 7 Числа наблюдений n₁, n₂,… n_k- называются частотами.

    Опр. 8 Отношение частоты к объему выборки называют относительной частотой.

 Обозначается:

Замечание: Сумма относительных частот равна 1.

Изучение выборки начинают с составления статистического распределения – таблицы с двумя строками. В одной строке указывается значения признака, в другой – соответствующие им частоты.

Опр. 9Статистическим распределением выборки называют таблицу значений признака расположенных в возрастающем порядке, и соответствующих им частот или относительных частот.

Различают два вида статистических распределений:

а) статистическое распределение выборки, представленное в виде таблицы, в первой строке которой перечислены все возможные варианты, а во второй – соответствующие им частоты называют д искретным вариационным рядом;

б) статистическое распределение выборки, представленное в виде таблицы, в первой строке которой находится последовательность интервалов а во второй – соответствующая частота, равная сумме всех частот вариант, попавших в данный интервал, называется интервальным вариационным рядом.

Составление статистического распределения начинают с определения наименьшего и наибольшего значений признака. Остальные записывают между ними в порядке возрастания. Далее подсчитывают частоты каждого значения признака.

Для непрерывно варьирующего количественного признака интервал его изменения разбивают на частичные интервалы одинаковой длины.  

Например. 1. Через каждый час измерялось напряжение тока в электросети. При этом были получены следующие значения (в В): 227, 219, 215, 230, 232, 223, 215, 218, 219, 227. построить по полученным данным дискретный вариационный ряд.

Решение:

	215	218	219	223	227	230	232
	2	1	2	1	2	1	1

.

2. Дан дискретный вариационный ряд

	1	3	6	8	9	13	15	20
	2	4	5	3	2	1	1	3

Построить интервальный ряд с шагом  для частот и относительных частот.

Решение:

	1-4	4-7	7-10	10-13	13-16	16-19	19-22
	6	5	5	1	1	0	3

	1-4	4-7	7-10	10-13	13-16	16-19	19-22
						0

.