
| 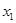
| 
| 
| ….. | 
|

| 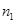
| 
| 
| ….. | 
|
Пусть известно статистическое распределение частот количественного признака 
Введем следующие обозначения:
 - частота наблюдений, при которых наблюдалось значение признака, меньшее некоторого заданного значения
- частота наблюдений, при которых наблюдалось значение признака, меньшее некоторого заданного значения  (накопленная частота);
(накопленная частота);
 - общее число наблюдений (объем выборки).
- общее число наблюдений (объем выборки).
Тогда, относительная частота события  равна
равна 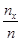 . Если
. Если  изменяется, то будет изменяться и относительная частота, то есть относительная частота
изменяется, то будет изменяться и относительная частота, то есть относительная частота 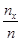 является функцией переменной
является функцией переменной  . Так как эта функция находится эмпирическим (опытным) путем, то ее называют эмпирической функцией распределения.
. Так как эта функция находится эмпирическим (опытным) путем, то ее называют эмпирической функцией распределения.
Опр. 10Эмпирической функцией распределения выборки называют функцию F*(x), определяющую для каждого значения  относительную частоту события
относительную частоту события  :
:  .
.

| 2 | 6 | 10 |

| 12 | 18 | 30 |
Пример. Построить эмпирическую функцию по данному распределению выборки:
Решение:
Найдем объем выборки  .
.
Найдем значение функции на всех промежутках изменения переменной  .
.
Пусть  , например
, например 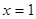 , тогда
, тогда  .
.
Пусть  , например
, например  , тогда
, тогда  .
.
Пусть  , например
, например  , тогда
, тогда  .
.
Пусть 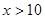 , например
, например  , тогда
, тогда  .
.
Искомая эмпирическая функция имеет вид:
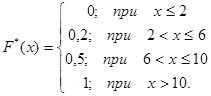
В отличие от эмпирической функции распределения, функцию распределения генеральной совокупности называют теоретической функцией распределения и обозначают  . Различие между эмпирической и теоретической функцией состоит в том, что теоретическая функция определяет вероятность события
. Различие между эмпирической и теоретической функцией состоит в том, что теоретическая функция определяет вероятность события  , а эмпирическая функция – относительную частоту этого же события. Но при достаточно больших
, а эмпирическая функция – относительную частоту этого же события. Но при достаточно больших  функции
функции  и
и 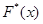 мало отличаются друг от друга, то есть, эмпирическая функция может служить оценкой для теоретической функции распределения.
мало отличаются друг от друга, то есть, эмпирическая функция может служить оценкой для теоретической функции распределения.
Свойства эмпирической функции распределения.
1. 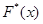 – неубывающая.
– неубывающая.
2. Значения эмпирической функции принадлежат промежутку [0;1].
3. Если  - наименьшая варианта, то
- наименьшая варианта, то 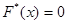 при
при  .
.
Если  - наибольшая варианта, то
- наибольшая варианта, то 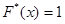 при
при  .
.
 2020-04-12
2020-04-12 284
284








