Статистическое распределение выборки изображается графически в виде полигона и гистограммы.
Опр. 11Полигоном частот называют ломаную, отрезки которой соединяют точки 
Для построения полигона частот на оси абсцисс откладывают значения вариант  , а на оси ординат - соответствующие им частоты
, а на оси ординат - соответствующие им частоты  Точки
Точки  соединяют отрезками прямых и получают полигон частот.
соединяют отрезками прямых и получают полигон частот.
Замечание. Аналогично строится полигон относительных частот, отмечаются точки с координатами  и соединяются прямыми линиями.
и соединяются прямыми линиями.
Например.

| 1 | 2 | 3 | 5 |

| 4 | 2 | 3 | 1 |

| 1 | 2 | 3 | 5 |

| 0,4 | 0,2 | 0,3 | 0,1 |
По данному распределению выборки построить полигон частот и относительных частот.


Полигоном обычно пользуются в случае небольшого числа вариант. В случае большого числа вариант и в случае непрерывного распределения признака чаще строят гистограмму. Для этого интервал, в котором заключены все наблюдаемые значения признака, разбивают на несколько частичных интервалов длинной  и находят для каждого частичного интервала сумму частот вариант
и находят для каждого частичного интервала сумму частот вариант  попавших в
попавших в  ый интервал. Затем, на этих интервалах, как на основаниях, строят прямоугольники с высотой
ый интервал. Затем, на этих интервалах, как на основаниях, строят прямоугольники с высотой  или
или  .
.
Опр. Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною h, а высоты равны отношению  , которое называют плотностью частоты.
, которое называют плотностью частоты.
Для построения гистограммы частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки параллельные оси абсцисс на расстоянии  .
.
Площадь  -го частичного прямоугольника равна
-го частичного прямоугольника равна  , то есть сумме частот вариант
, то есть сумме частот вариант  - го интервала. Площадь всей гистограммы частот равна сумме всех частот, т.е, объему выборки.
- го интервала. Площадь всей гистограммы частот равна сумме всех частот, т.е, объему выборки.
Например. Построить гистограмму частот по следующим данным

| 5-10 | 10-15 | 15-20 | 20-25 | 25-30 | 30-35 | 35-40 |

| 4 | 6 | 16 | 36 | 24 | 10 | 4 |

| 0,8 | 1,2 | 3,2 | 7,2 | 4,8 | 2 | 0,8 |

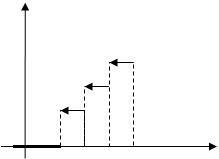
График эмпирической функции распределения тоже имеет ступенчатый вид и имеет точки разрыва.
Пример.
Построим график эмпирической функции распределения вида 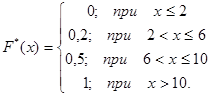 .
.
 |
 2020-04-12
2020-04-12 312
312








