2020-04-12
1880
План:
1. Понятия генеральной и выборочной средней и методы их расчета.
2. Оценка генеральной средней по выборочной средней.
1. Пусть изучается дискретная генеральная совокупность относительно количественного признака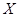 
.
Определение 1. Генеральной средней 
называют среднее арифметическое значений признака генеральной совокупности.
Если все значения 
признака генеральной совокупности объема 
различны, то
.
Если же значения признака 
имеют соответственно частоты 
, причем 
, то
или 
.
Пусть все значения различны. Так как каждый объект может быть извлечен с одной и той же вероятностью 
, то можно найти математическое ожидание признака :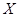
.
Итак, если рассматривать обследуемый признак генеральной совокупности как случайную величину, то математическое ожидание признака равно генеральной средней этого признака, то есть
.
Такой же итог будет получен, если допустить, что генеральная совокупность содержит по нескольку объектов с одинаковым значением признака.
Обобщая полученный результат на генеральную совокупность с непрерывным распределением признака 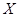, полагают, что генеральная средняя равна математическому ожиданию, то есть
.
Пусть для изучения генеральной совокупности относительно количественного признака 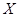произведена выборка объема 
.
Определение 2. Выборочной средней 
называют среднее арифметическое значений выборочной совокупности.
Если все значения 
признака выборочной совокупности объема 
различны, то
.
Если же значения признака 
имеют соответственно частоты 
, причем 
, то
или 
.
Пример. Выборочным путем были получены сведения о сдаче одного экзамена 15 человек с факультета из 50: 5, 4, 5, 3, 4, 3, 3, 5, 5, 4, 4, 5, 3, 3, 4. построить дискретный вариационный ряд и найти выборочную среднюю.
Решение.
 | 3 | 4 | 5 |
 | 5 | 5 | 5 |
.
- средняя оценка на экзамене.
2. Пусть из генеральной совокупности извлечена повторная выборка объема со значениями признака 
. Будем считать эти значения признака различными.
Пусть генеральная средняя неизвестна и требуется найти ее по данным выборки. В качестве оценки генеральной средней принимают выборочную среднюю
.
Покажем, что 
- несмещенная оценка, то есть докажем равенство
.
Будем рассматривать как случайную величину и 
- как независимые, одинаково распределенные случайные величины 
. Поскольку эти величины одинаково распределены, то они имеют одинаковое математическое ожидание, которое обозначим через 
. Так как математическое ожидание среднего арифметического одинаково распределенных случайных величин равно математическому ожиданию каждой из величин, то
.
Приняв во внимание, что каждая из величин имеет то же распределение, что и генеральная совокупность, можно отметить, что и числовые характеристики этих величин и генеральной совокупности одинаковы. Тогда, математическое ожидание каждой из величин равно математическому ожиданию признака 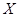генеральной совокупности, то есть
, следовательно 
.
Таким образом, мы доказали, что выборочная средняя является несмещенной оценкой генеральной средней.
