Расчет переходных процессов на стыке линий

Так как линия без потерь, то для падающих волн в любой точке первой линии (до которой они дошли) имеем:

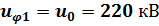
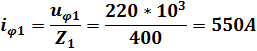
В любой точке первой линии напряжение и ток можно представить в виде суммы падающей и отраженной волн: ; :

                               

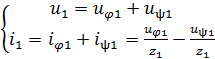
где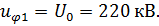

 Из этих уравнений вытекает соотношение 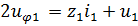 – напряжение на входе четырехполюсника.

На выходе же имеем: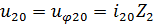

Данным  уравнениям формально удовлетворяет схемная модель с сосредоточенными параметрами (рис.3)

Особенность данной расчетной схемы состоит в том, что напряжение на ее входе равно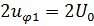

 

Рис. 3

Эта расчетная модель справедлива для определения закона изменения напряжений и токов в функции времени только в месте стыка линий, т.е. на зажимах четырехполюсника. Входящие в нее волновые сопротивления Z₁ учитывает влияние первой линии, Z₂ учитывает влияние второй линии вплоть до момента прихода к месту стыка отраженной от нагрузки волны, т.е. пока

,

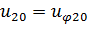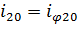
Т.к. схема содержит один реактивный элемент и параллельно подключенный к нему резистор, рассчитаем переходный процесс.

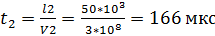  – время, за которое волна дойдет до двухполюсника

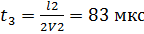 – время, за которое отраженная волна пройдет половину второй линии

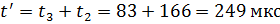 – время начала переходного процесса в четырехполюснике.

Рассчитаем переходный процесс (без составления дифференциального уравнения) при подключении линии к сети:

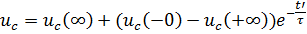
1. Найдем переменные состояния до замыкания ключа, (цепь в установившемся режиме до коммутации)  :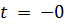

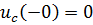
  2. По законам коммутации:   

3.В установившемся режиме после коммутации конденсатор может рассматриваться как разрыв, тогда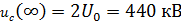

3.1. Найдём постоянную времени 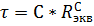, где  – эквивалентное сопротивление относительно зажимов конденсатора С, при замене источников их эквивалентными сопротивлениями. Таким образом,

 

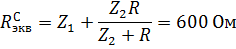
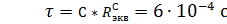
Таким образом,

 

4. Выразим остальные напряжения и токи:

 

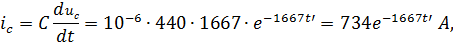
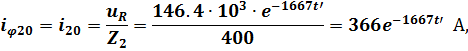
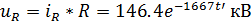
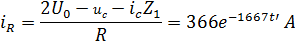
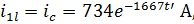
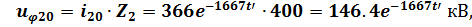
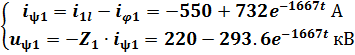
Часть 2.Переходный процесс в нагрузке.