Диференціальні рівняння рівноваги в прямокутній системі координат

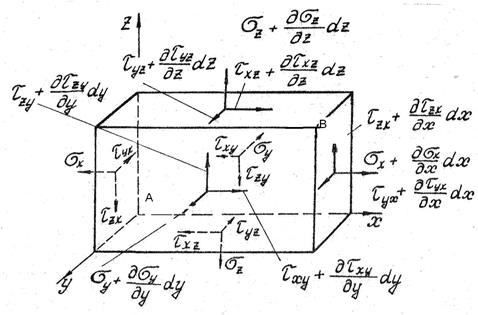
Як витікає з принципу локальності самоврівноважені навантажень, напруги безперервно змінюються за об’ємом тіла і є безперервними функціями координат. При цьому кожен елементарний об'єм повинен знаходитися в рівновазі, динамічному (з урахуванням сил інерції) або статичному (без урахування сил інерції). Розглянемо напружений стан двох сусідніх точок А і В, що перебувають на нескінченно близьких відстанях dx, dy, dz один від одного (Рис.20; куб на малюнку не матеріальна точка; він характеризує відстані між точками А і В за об’ємом). Лівий нижній куткуба відповідаєточці А, напруги в її околицях діють на невидимих площадках куба.

Рис.20. Напружений стан в двох сусідніх точках А і В

Нехай вони задані звичайним тензором напружень Т_σА. Тоді напружений стан точки В задано тензором Т_σВ, компоненти якого відрізняються від компонент тензора Т_σА нескінченно малими приростами, які діють на видимих площадках. Запишемо ці тензори:

                                    Т_σА = _,

Т_σВ = .

              

Приріст кожної компоненти напружень тензора Т_σВ визначені так само, як показано в розділі 3.4.1 для зміщень (частна часткової похідної функції даної напруги уздовж даної осі на диференціал з цієї ж осі). Розглянемо рівновагу сил, що діють на даний об`єм. Для того щоб від напруг перейти до сил, потрібно кожну компоненту напруг помножити на площу її дії.

Суму сил, що діють по осі х, можна скласти рис. 3.20, але найбільш просто це зробити, використовуючи тензори напруг. У верхніх рядках кожного з тензорів розташовані компоненти, що діють уздовж осі х. Другий індекс кожної компоненти відповідає площадці її дії, що дозволяє розрахувати її площу як добуток двох розмірів куба на рис.20. Врахуємо, що для рівноваги елемента необхідно, щоб компоненти кожного з тензорів були направлені в різні сторони (див. рис.20.). Отримаємо

ΣX = [σ_x + (∂σ_x/∂x)dx]dydz - σ_xdydz + [τ_xy + (∂τ_xy /∂y)dy]dzdx - τ_xydzdx +

                     + [τ_xz + (∂τ_xz /∂z)dz]dxdy - τ_xzdzdx = 0.

Розкриємо дужки і скоротимо на dxdydz, отримаємо

              ∂σ_x/∂x + ∂τ_xy /∂y + ∂τ_xz /∂z = 0.

Рівняння рівноваги сил з інших осей ΣУ = 0 і ΣZ = 0 знайдемо за двома іншими рядками тензорів. У результаті отримуємо систему з трьох диференціальних рівнянь, що містять (з урахуванням закону парності дотичних напружень) 6 невідомих - 3 нормальних і три дотичних напруги

∂σ_x/∂x + ∂τ_xy /∂y + ∂τ_xz /∂z = 0;

∂τ_yx/∂x + ∂σ_y/∂y + ∂τ_yz/∂z = 0;                                                    (66)

∂τ_zx /∂x + ∂τ_zy /∂y +∂σ_z/∂z = 0.

Рівняння (66) визначають зв'язок між приростами компонент напружень, що діють уздовж кожної осі в довільній системі координат. Їх називають статичними рівняннями рівноваги, тому що в них не враховано сил інерції. Для полегшення запам'ятовування відзначимо, що ліва частина рівнянь складається з похідних компонентів звичайного тензора напружень за індексами площадок їх дії. Рівняння (66) статично невизначні, тому що містять 6 невідомих у трьох рівняннях.

У разі необхідності використовують динамічні рівняння рівноваги, що враховують сили інерції і інші об'ємні сили

∂σ_x/∂x + ∂τ_xy /∂y + ∂τ_xz /∂z + X_ρ = ρ∂²u_x/∂t²

∂τ_yx/∂x + ∂σ_y/∂y + ∂τ_yz/∂z + Y_ρ= ρ∂²u_y/∂t²                                                 (67)       

∂τ_zx /∂x + ∂τ_zy /∂y +∂σ_z/∂z + Z_ρ= ρ∂²u_z/∂t²

У рівняннях (67) X_ρ, Y_ρ, Z_ρ-проекції об'ємної сили на осі, віднесеної до маси, ρ - щільність деформівного матеріалу. Праві частини рівнянь містять проекції сил інерції за координатним осям.

 

Плоскі задачі

Рішення об'ємних задач складне і займає багато часу. Для полегшення рішення спрощують схему процесу, приймаючи, що або одна головна напруга дорівнює нулю (плоский напружений стан), або одна з головних деформацій дорівнює нулю (плоский деформований стан). Обидва ці підходи об'єднують загальною назвою «плоскі задачі». У деяких випадках плоский стан реально має місце. Наприклад, при розтягуванні листа напругами, нормальними до його периметру (рис.21),

 

Рис.21. Схема плоскої задачи

відсутні напруги, нормальні до його поверхні, і завдання є плоскою напруженою. Якщо плинність металу завширшки заборонено стінками інструменту, його розміри зменшуються по висоті і збільшуються по довжині. В інших випадках просто нехтують наявністю однієї з компонент напружень або деформацій, якщо їх величина помітно менше в порівнянні з іншими компонентами. Такі випадки широко поширені на практиці.

Плоскі завдання мають такі особливості:

- Компоненти напруг і деформацій не залежать від однієї з координат і залишаються постійними вздовж цієї координати;

- Єдине значення компоненти вимагає, щоб ця компонента була головною;

- Майданчики, нормальні до цієї компоненті, є головними майданчиками, на них відсутні дотичні напруги; всі компоненти дотичних напружень з індексом цієї осі дорівнюють нулю (дотичні напруги з другим індексом, відповідним даної головному майданчику, відсутні, а дотичні напруги з напрямком даної осі дорівнюють нулю внаслідок парності дотичних напружень).

- Головне нормальне напруження по цій осі або дорівнює нулю (плоске напружений стан), або дорівнює напівсумі двох інших головних напруг (плоске деформований стан).

Останнє положення випливає з аналізу девіаторной схеми напруг (див. 3.3.5). Деформація по осі 2 відсутній, якщо друга компонента девіатора дорівнює нулю, тобто σ₂ = σ_ср. Так як

σ_ср = (σ₁ + σ₂ + σ₃)/3 = (σ₁ + σ_ср + σ₃)/3, откуда σ_ср = (σ₁ + σ₃)/2.

Рішення плоских задач значно простіше в порівнянні з об'ємними. З статичних і геометричних рівнянь виключаються компоненти, що містять індекс другої осі (при вирішенні в головних осях) або індекс у (при вирішенні в довільних осях, зазвичай віссю відсутності компоненти беруть вісь у). Система диференціальних рівнянь рівноваги складається з двох рівнянь, що містять три невідомі (σ_х, σ_z, τ_xz)

∂σ_x/∂x + ∂τ_xz/∂z = 0;                                                                        (68)

∂τ_zx /∂x +∂σ_z/∂z = 0.

З шести геометричних рівнянь зберігаються лише три        

            ε_х = ∂u_x/∂х, ε_z = ∂u_z/∂z, γ_zx = ∂u_x/∂z + ∂u_z/∂x.             (69)

Тензори напруг і деформацій у головних осях мають вигляд для плоского напруженого стану

Т_σ = 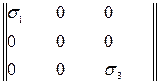; Т_ε = ; D_σ = ,         

для плоского деформованого стану

     Т_σ =  ;  Т_ε = ; D_σ =  .   

При цьому ε₁ = - ε₃, σ₂ = (σ₁ + σ₃)/2 = σ_ср.

Якщо σ₁ =-σ_3, то σ_ср=0, в цьому випадку має місце одночасно і плоске напружене і плоске деформований стан (друга компонента девіатора напруг дорівнює нулю, так як σ₂=σ_ср=0), тензор напружень дорівнює девіатора напруг. Умова ε₁=-ε₃ зберігається. Таке напружено-деформований стан називають чистим зрушенням.