Осесиметрична завдання

Розгляд будь-яких тіл обертання, навантаження до яких прикладено симетрично щодо їх осі симетрії, називають осесиметричними. Вирішення таких задач також простіше, ніж рішення об'ємних. Але розглядати осесиметричні задачи зручніше не в прямокутній, а в циліндричній системі координат. У цій системі положення точки визначається радіусом-вектором ρ, кутом θ і аплікатою z (Рис.22).

Рис. 3.22. Циліндрична система координат та індексація напружень у цій системі

 

 

Напружений стан в загальному вигляді описується тензором напружень

                            Т_σ = 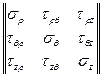.                                         (70)

Напруга σ_ρ називають радіальним, σ_θ - тангенціальним, σ_z - осьовим.

Для осесиметричного напруженого стану внаслідок симетрії тіла і зовнішніх навантажень направлення всіх радіусів рівноправні. Тому складові напруг і деформацій не залежать від кута θ, площадки θ є головними, дотичні компоненти, що містять індекс θ, дорівнюють нулю (одні тому що площадка головна, інші за законом парності дотичних напружень). Звідси тензор напружень для осесиметричної задачі в циліндричній системі координат має вигляд

                               Т_σ = .                                              (71)

Для виведення диференціальних рівнянь рівноваги розглянемо елементарний об'єм з розмірами dρ, dθ, dz (Рис.23), у якого компоненти напружень на невидимих гранях визначають напружений стан точки А, а на видимих - точки В. Тензори напруг Т_σА і Т_σВ мають вигляд

Т_σА = , Т_σВ = .

Рис. 3.23. Рівновага елементарного об'єму

             для осесиметричної задачі   

 

Складемо рівняння рівноваги сил, що діють на елементарний об'єм, показаний на Рис.23 Попередньо запишемо вираження, що визначають площі його граней, враховуючи, що довжина дуги дорівнює добутку радіуса на кут, що відповідає цій дузі. Шукані площі показані на Рис.24:

   площа аbcd = F_ρ = ρdθdz (ρdθ – довжина дуги bс);

   площа а'b'c'd' = F_{(ρ + dρ)} = (ρ + dρ)dθdz ((ρ + dρ)dθ – довжина дуги b'с');

   площа аbb'a' = площі dcc'd' = F_θ = dρdz;

   площа bcc'b' = площі add'a' = F_z = (ρ + dρ/2)dθdρ ≈ ρdθdρ.

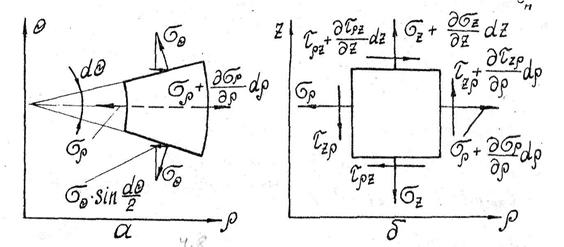
Рис.24. Проекції елементарного об'єму на площині ρ0θ и ρ0z.

 

Складемо рівняння рівноваги сил, що діють на елемент вздовж осі ρ. У рівняння увійдуть не тільки сили, створені компонентами, що стоять у верхніх рядках тензорів Т_σА і Т_σВ, але і проекції напруги σ_θ на вісь ρ-2_σθsin(θ/2) (коефіцієнт 2, так як таких проекцій дві - рис.24. Обидві проекції спрямовані проти позитивного напрямку осі ρ і мають знак мінус, як і компоненти тензора Т_σА. Множачи компоненти напружень на площу їх дії, отримуємо

ΣΡ = [σ_ρ + (∂σ_ρ/∂ρ)dρ] (ρ + dρ)dθdz - σ_ρρ dθdz + [τ_ρz + (∂τ_ρz/∂z) dz] ρdθdρ –

- τ_ρzρdθdρ - 2σ_θ sin(dθ/2)dρdz = 0.

    Розкриваючи дужки і приймаючи, що sin(dθ/2) ≈ dθ/2, маємо

σ_ρρdθdz +σ_ρdρdθdz + [(∂σ_ρ/∂ρ)dρ]ρdθdz + (∂σ_ρ/∂ρ)dρ²dθdz - σ_ρρ dθdz +

+ τ_ρzρdθdρ + (∂τ_ρz/∂z)dzρdθdρ - τ_ρzρdθdρ - 2σ_θ (dθ/2) dρdz = 0.

    Після приведення подібних доданків, виключення (∂σ_ρ/∂ρ)dρ²dθdz як нескінченно малою вищого порядку, і скорочення на dρdθdz, отримаємо

           σ_ρ + (∂σ_ρ/∂ρ)ρ + (∂τ_ρz/∂z)ρ - σ_θ = 0.                             (72, а)

    Складемо рівняння рівноваги сил, що діють на елементарний об'єм по осі z (см. Рис.23, чи нижче строки тензорів Т_σА і Т_σВ)         

 [(τ_zρ+ ∂τ_zρ/∂ρ)dρ](ρ + dρ)dθdz - τ_zρ ρdθdz + [σ_z+ (∂σ_z/∂z)dz] ρdθdρ – σ_zρdθdρ = 0.

Розкриємо дужки

τ_zρρdθdz + τ_zρdρdθdz + (∂τ_zρ/∂ρ)dρ(ρ)dθdz + (∂τ_zρ/∂ρ)dρ²dθdz - τ_zρρdθdz +

σ_zρdθdρ + (∂σ_z/∂z)dz ρdθdρ - σ_zρdθdρ = 0.

Після приведення подібних, виключення нескінченно малою вищого порядку (∂τ_zρ/∂ρ)dρ²dθdz і скорочення на dρdθdz, отримаємо

                 τ_zρ+ (∂τ_zρ/∂ρ)ρ + (∂σ_z/∂z)ρ = 0.                                          (72, б)

Після перетворення рівнянь (72, а) і (72, б) отримуємо систему з двох диференціальних рівняння з чотирма невідомими (σ_ρ, σ_θ, σ_z і τ_zρ = τ_ρz)

∂σ_ρ/∂ρ + ∂τ_ρz/∂z + (σ_ρ - σ_θ)/ρ = 0;                                                     (73)

 ∂τ_zρ/∂ρ + ∂σ_z/∂z + τ_zρ/ρ = 0.

Для визначення зв'язку між зміщеннями та деформаціями по осі θ розглянемо лінійний елемент ab, який в результаті деформації зміщується в положення a'b' (рис.25). Відносна умовна деформація по осі θ складе

ε_θ = (a'b' – ab)/ab = [(ρ - u_ρ)dθ – ρdθ]/ρdθ = u_ρ/ρ.   

 

Рис.25. Деформації і зміщення вздовж осі

            θ в осесиметричній задачі

 

Зв'язок між зміщеннями та деформаціями по осях ρ і z і в площині ρ0z має вигляд, аналогічний рівнянню (69). Разом з попереднім рівнянням маємо

 

ε_ρ = ∂u_ρ/∂ρ, ε_θ = u_ρ/ρ, ε_z =∂u_z/∂z, γ_ρz = ∂u_z/∂ρ+ ∂u_ρ/∂z.                   (74)   

Система (74) являє собою геометричні рівняння для осесиметричної задачі. Вона містить 6 невідомих - 4 деформації і два зміщення і є статично невизначеної. Решта зсувні деформації, як і дотичні напруження, дорівнюють нулю.

Рівняння нерозривності деформації має вигляд

∂ε_θ/∂ρ = (ε_ρ - ε_θ)/ρ.                                                                            (75)