2020-04-20
212
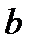
A + 
B + 
C = 180°
если BC >AB, то 
A > 
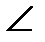C
2. Признаки равенства и подобия треугольников.
1). Два треугольника равны, если у них равны:
а) две стороны и угол между ними
б) два угла и сторона, заключенная между ними
в) три стороны.
Два треугольника называются равными, если при наложении они совпадают
2). Два треугольника подобны, если у них:
а) два угла равны
б) две стороны пропорциональны и углы между ними равны
в) три стороны пропорциональны.
Два треугольника называются подобными, если у них углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого треугольника.
Сходственные стороны в подобных треугольниках - стороны, лежащие против равных углов.
Коэффициент подобия – отношение сходственных сторон.
3). В подобных треугольниках:
а) периметры подобных треугольников относятся как коэффициент подобия
б) площади подобных треугольников относятся как коэффициент подобия в квадрате.
B
N
A C M P
Δ ABC 
Δ MNP 
Формулы площадей треугольника
1). Равносторонний треугольник
S = 
a – сторона треугольника
h =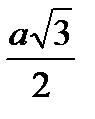 
h – высота треугольника
2). Прямоугольный треугольник
S = 
a b a, b – катеты треугольника
3). Разносторонний треугольник
S = a h a – сторона треугольника
h – высота, проведенная к этой стороне
S = a b sin α a, b – стороны треугольника
α - угол между этими сторонами
S = 
a, b, c – стороны треугольника
p – полупериметр; p = (a + b + c)
S = 
a, b, c – стороны треугольника
R – радиус описанной окружности
S = P r P –периметр треугольника
r – радиус вписанной окружности
Решение треугольников.
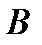
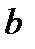
1). Теорема синусов:
Стороны треугольника пропорциональны синусам противолежащих углов.
Отношение стороны треугольника к синусу противолежащего угла равно удвоенному радиусу описанной окружности.
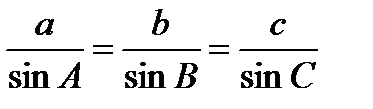
2). Теорема косинусов:
Квадрат стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.
Прямоугольные треугольники.
