2020-04-20
149
в) односторонние углы в сумме дают 180°
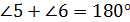
Опорные задачи.
1). Биссектрисы смежных углов перпендикулярны.
если MB и BN – биссектрисы 
ABD и DBC, то 
(
МBN = 90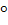 
)
2). Точка, лежащая на биссектрисе угла, равноудалена от сторон угла.
если AM – биссектриса угла A
то MK=MN, (MK 
AB и MN 
AC).
3). Точка, лежащая на серединном перпендикуляре отрезка, равноудалена от концов этого отрезка.
Серединный перпендикуляр отрезка – это прямая, перпендикулярная к отрезку и проходящая через его середину.
.
если MH – серединный перпендикуляр отрезка AB,
то MA = MB.
4). Перпендикуляр,наклонная и проекция.
МН – перпендикуляр,
AH – проекция наклонной MA,
ВН –проекция наклонной MB,
если MB >MA,то ВH > АH и если MB = MA, то ВH = АH
|
|
|
Тема 1.2. Треугольник
1. Свойства
1). В равностороннем треугольнике все стороны равны, а углы равны по 60 
2). В равнобедренном треугольнике углы при основании равны и биссектриса, медиана и высота, проведенные к основанию, совпадают.
,
Средняя линия в треугольнике параллельна основанию и равна его половине.
Средняя линия соединяет середины боковых сторон треугольника.
B
если MN – средняя линия,
M N то MN 
AC и MN = 
AC
A C
4). Внешний угол треугольника равен сумме двух других углов, не смежных с ним.
Внешним углом треугольника называется угол, смежный с каким-либо углом треугольника.
BCD 
= 180 
- BCА
BCD = 
A + 
B
5). В любом треугольнике выполняются следующие условия:
а) сумма углов равна 180°
Б) против большей стороны лежит больший угол
