













Пифагоровы тройки:
3, 4, 5 6, 8, 10 9, 12, 15 3n, 4n, 5n (n – натуральное число)
5, 12, 13 5n, 12n, 13n и другие.









2). Опорные прямоугольные треугольники 




















30 
|
45 
|
Нахождение всех функций углов прямоугольного треугольника по одной из них
В 
 ВС = 2х и ВА = 3х
ВС = 2х и ВА = 3х
2х 3х АС  =
=  =
= 
 С
С  А
А  tgА
tgА 
В tgА  3
3  ВС = 3х и СА = 1х
ВС = 3х и СА = 1х

Х
 АВ
АВ  =
=  =
= 
С А
х


Образцы решения задач
1. В прямоугольном треугольнике ABC  . Найти
. Найти  и
и

Если  . Тогда
. Тогда 
 и
и 
2. В прямоугольном треугольнике  , катет BC равен 9. Найти длину гипотенузы AB.
, катет BC равен 9. Найти длину гипотенузы AB.



 Т.к. дан противолежащий катет, надо найти
Т.к. дан противолежащий катет, надо найти 

 =
= 
Т.к. 

3. В равнобедренном треугольнике АВС АС = ВС = 10, АВ =  . Найти
. Найти 
С
А
А
10 10

А 4  H В
H В
Т.к. треугольник равнобедренный АН = HВ  = 4
= 4 
Чтобы найти  , надо найти противолежащий катет СН
, надо найти противолежащий катет СН
СН = 

4. В прямоугольном треугольнике  катет ВС = 2. Найти длину высоты СН, опущенной на гипотенузу.
катет ВС = 2. Найти длину высоты СН, опущенной на гипотенузу.

 В
В  1 способ: в
1 способ: в 
H


2
 СА =
СА = 
С А СН  =
= 
2 способ: в  ВСН
ВСН 
СН = 
5. Найти стороны треугольника
4 8 10 3  6
6 
 30
30  5
5 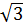 3
3

 4
4 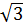 45
45 
 60
60  3 6
3 6
5
 4). Признаки равенства прямоугольных треугольников
4). Признаки равенства прямоугольных треугольников
Два прямоугольных треугольника равны, если у них равны:
а) катет и гипотенуза
б) гипотенуза и острый угол
Соотношение в прямоугольном треугольнике















Описанные и вписанные треугольники
1). Положение центра окружности.
а). Центром вписанной в треугольник окружности является точка пересечения биссектрис треугольника.
Радиус вписанной окружности – перпендикуляр, опущенный из этой точки на сторону треугольника.
б). Центром описанной около треугольника окружности является точка пересечения серединных перпендикуляров треугольника.
Радиус описанной окружности –отрезок, соединяющий центр окружности с вершиной треугольника
в). В равностороннем треугольнике центр вписанной и описанной окружностей совпадают
. 2). Формулы радиусов окружности
а) равносторонний треугольник б) прямоугольный треугольник
.




















в) разносторонний треугольник








Опорные задачи.
1). Свойство медианы в прямоугольном треугольнике:
медиана в прямоугольном треугольнике равна половине гипотенузы.


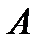

 если СМ – медиана
если СМ – медиана
CM =  AB или CM = AM = MB=R
AB или CM = AM = MB=R
М – центр описанной окружности


2). Свойство высоты в равнобедренном прямоугольном треугольнике:
высота в равнобедренном прямоугольном треугольнике равна половине
гипотенузы (т. к. высота в равнобедренном треугольнике является и медианой)
А
М СМ - высота
 CM =
CM =  AB или CM = AM = MB=R
AB или CM = AM = MB=R
С В  = 45
= 45 
3) Свойство биссектрисы треугольника:
биссектриса треугольника делит противоположенную сторону на
 2020-04-20
2020-04-20 177
177








