Дата: 06.04. Тема «Сочетания»
Цели: ввести понятие сочетания из п элементов по k (k ≤ п); вывести формулу нахождения числа сочетаний из п элементов по k; формировать умения решать комбинаторные задачи с применением данной формулы.
I. Устная работа.
1. З а д а ч а. В футбольном турнире участвуют несколько команд. Оказалось, что все они для трусов и футболок использовали белый, красный, синий, зеленый или желтый цвета, причем были представлены все возможные варианты.
а) Сколько команд участвовали в турнире?
б) Сколько команд играли в зеленых футболках?
в) У скольких команд футболки и трусы были разного цвета?
г) У скольких команд футболки и трусы были разного цвета, причем трусы были не красные?
2. Найти значение выражения:
а) Р 4 + Р 3; б) Р 6 – Р 5; в)  ; г)
; г)  ;
;
д) 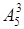 ; е)
; е) 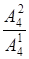 ; ж)
; ж) 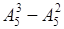 ; з)
; з) 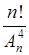 .
.
II. Изучение нового материала. (Краткий конспект)
1. практическая задача:
«Сколькими способами можно смешать по три краски из имеющихся пяти?».
Р е ш е н и е
Обозначим имеющиеся краски буквами латинского алфавита a, b, c, d, e. Выпишем возможные варианты смешивания красок, учитывая, что от порядка расположения красок результат не зависит:
abc, abd, abe, ace, ade
bcd, bce, bde
cde
Мы указали различные способы смешивания красок, в которых по-разному сочетаются три краски из данных пяти. Говорят, что мы составили все возможные сочетания из 5 элементов по 3.
2. Определение. Сочетанием из п элементов по k называют любое множество, составленное из k элементов, выбранных из данных п элементов.
П о д ч е р к и в а е м, что, в отличие от размещений, в сочетаниях не имеет значения, в каком порядке указаны элементы. Два сочетания из п элементов по k отличаются друг от друга хотя бы одним элементом.
3. Обозначение. 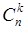 (читается «С из п по k»).
(читается «С из п по k»).
В рассмотренном примере мы нашли, что  = 10.
= 10.
4. Вывод формулы числа сочетаний из п по k, где k ≤ п.
В отличие от предыдущих тем, при доказательстве мы опираемся не напрямую на комбинаторное правило умножения, а на ранее выведенные формулы числа перестановок и размещений.
Сперва замечаем, что 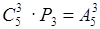 (по комбинаторному правилу умножения), значит,
(по комбинаторному правилу умножения), значит, 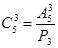 .
.
И затем проводим аналогичные рассуждения для общего случая:

Учитывая, что  , где п ≤ k, получаем, что
, где п ≤ k, получаем, что
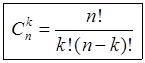
| – формула вычисления числа сочетаний из п по k, где k ≤ п. |
5. Рассматриваем примеры задач на нахождение числа сочетаний из учебника на с. 184–185.
 2020-05-11
2020-05-11 139
139







