2020-05-11
91
Закономерности случайных событий изучает специальный раздел математики – теория вероятностей. В учебнике нет определения понятия «исход случайного события». Можно оперировать таким: исход – возможный результат опыта (эксперимента).
Следует хорошо отличать события от исходов, что в дальнейшем позволит избежать многих трудностей при введении понятия вероятности случайного события.
Далее рассматриваем пример из учебника со с. 188.
И с х о д ы и с п ы т а н и я: 1. Выпадает одно очко.
2. Выпадает два очка.
3. Выпадает три очка.
4. Выпадает четыре очка.
5. Выпадает пять очков.
6. Выпадает шесть очков.
С л у ч а й н о е с о б ы т и е: 1. Выпадет шесть очков.
На этом примере наглядно демонстрируем, что исход испытания – значение наблюдаемого признака (количество очков), непосредственно полученное по окончании эксперимента (каждый эксперимент заканчивается одним и только одним исходом). Событие – появление исхода, обладающего заранее указанным свойством (шесть очков).
Затем вводим понятия «частота события» и «относительная частота события».
В в о д и м ы е о б о з н а ч е н и я:
А – событие;
т – число испытаний, при которых произошло событие А;
п – общее число испытаний;
W (A) =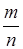 
– относительная частота случайного события.
П р о б л е м н ы й в о п р о с: Почему важна относительная частота события? Приведите пример. (Иван попал в мишень три раза, Петр – четыре. Кто из них лучше стреляет? Можно ответить, что Петр – лучше, так как больше число попаданий. Но мы не знаем, сколько у каждого было попыток. Например, Иван сделал всего три выстрела и попал все три раза, относительная частота попадания W (A) = 
= 1. А Петр сделал серию из 20 выстрелов и попал всего четыре раза: W (A) = 
= 0,2.)
