Способы решения показательных уравнений

• Простейшее уравнение  имеет решение .
• Уравнение вида  логарифмированием по основанию a сводят к виду .
• Уравнение вида  равносильно уравнению .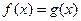
• Уравнение вида  через замену сводят к многочлену , а затем решают совокупность простейших показательных уравнений .
• Уравнение со взаимно обратными величинами  заменой  сводят к уравнению , а затем решают совокупности уравнений .
• Уравнения, однородные относительно  и  при условии  вида  через замену  сводят к многочлену , а затем решают совокупности уравнений

Способы решения логарифмических уравнений

• Простейшее уравнение  имеет решение .
• Уравнения вида  заменой  сводят к уравнению , а затем решают совокупность простейших уравнений .
• Уравнения вида  равносильно системе
• Уравнения вида равносильно системе
• Уравнения вида 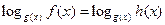равносильно системе

Примеры заданий показательных уравнений и достаточные знания свойств, необходимые для решения этих заданий.

Задания	Достаточные знания свойств	Формула
	Свойства степени  с отрицательным целым показателем
	Свойство равносильности показательных уравнений
	Свойство произведения степеней
	Свойство частного степеней

Примерное задание. Решить уравнение

Решение:  т.к. , то можно разделить на  обе части уравнения , получим . Пусть , тогда получим систему . Решая уравнение  получим корни  . Вернемся к замене и решим систему

Ответ:

Для решения используем последовательно знания следующих свойств:

ü Свойство произведения степеней с одинаковыми основаниями: .

ü Свойство степени, основанием которой является степень: .

ü Свойство степени произведения положительных чисел: .

ü Свойство равносильности уравнений  и :

ü Свойство частного степеней с одинаковыми показателями степени:

ü Основное свойство дроби: .

ü Свойство степени с нулевым показателем: .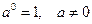

ü Свойство степени с отрицательным показателем: .