Решение тригонометрического уравнения состоит в выполнении преобразований, в результате которых исходное уравнение сводится к одному из простейших тригонометрических уравнений.
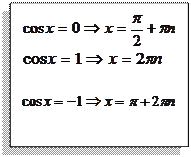 Простейшие тригонометрические уравнения
Простейшие тригонометрические уравнения
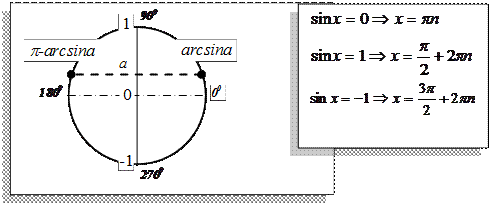
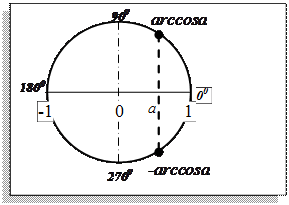 Частного вида
Частного вида
 |
Общего вида
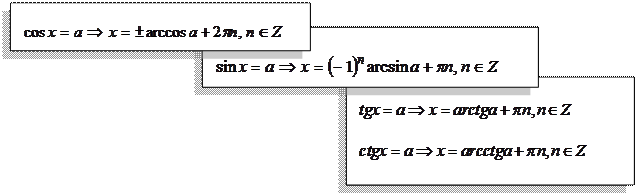
Запомнить. Уравнения 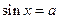 и
и 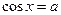
имеют решение только при условии 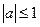 ,
,
а уравнения 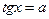 и
и 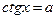 имеют решения
имеют решения
при любом 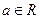 .
.
Способы решения тригонометрических уравнений
- Уравнения вида
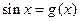 и
и 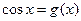 решаются с ограничением на x вида
решаются с ограничением на x вида 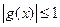 .
. - Уравнения вида
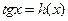 и
и 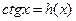 решаются без ограничений на x выражения
решаются без ограничений на x выражения 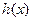 .
. - Уравнения вида
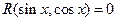 , где R – дробно-рациональная функция, решают
, где R – дробно-рациональная функция, решают
заменой переменной:
применяется универсальная подстановка 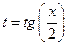 , тогда
, тогда 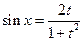 ,
, 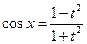 и исходное уравнение сводится к уравнению вида
и исходное уравнение сводится к уравнению вида 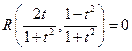 , а это уже многочлен
, а это уже многочлен 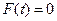 , затем решается совокупность уравнений
, затем решается совокупность уравнений 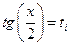 ;
;
введением вспомогательного аргумента:
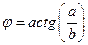 уравнения вида
уравнения вида 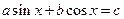 сводится к простейшему уравнению
сводится к простейшему уравнению 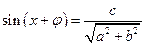 .
.
Замечание 1. При универсальной подстановке следует помнить, что 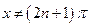 и поэтому надо проверить, не является ли
и поэтому надо проверить, не является ли 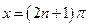 корнем исходного уравнения.
корнем исходного уравнения.
Замечание 2. Используют замену 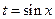 в уравнениях, которые не меняются при замене x на
в уравнениях, которые не меняются при замене x на 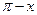 . Используют замену
. Используют замену 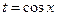 в уравнениях, которые не меняются при замене x на – x. Используют замену
в уравнениях, которые не меняются при замене x на – x. Используют замену 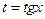 в уравнениях, которые не меняются при замене x на
в уравнениях, которые не меняются при замене x на 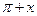 или однородных относительно
или однородных относительно 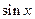 и
и 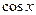 . Указанные замены сводят исходное уравнение к уравнению вида
. Указанные замены сводят исходное уравнение к уравнению вида 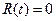 .
.
 2020-05-11
2020-05-11 153
153








